クォータニオン徹底解説

3Dゲームの開発でクォータニオンを使う本当の理由

クォータニオンを使うことによって、行列を使う場合に比べてメモリの使用量や計算量が少なくて済みそうですが、クォータニオンを使うメリットはそれだけでしょうか? メモリの使用量で言えばオイラー角を使った方が有利です。3Dゲームの開発において、どうしてもクォータニオンを使わなければいけない理由が別にあるのです。

例えば、ゲームのキャラクターが歩いているとします。このとき、キャラクターの手足の骨には「歩き」のアニメーションデータが適用されていて、このデータにどの時刻にどれだけ手足が回転するかという情報が入っています。

さて、このキャラクターが突然スライムに斬り掛かったとします。この場合、キャラクターの手足には「斬り掛かる」アニメーションが適用されるのですが、突然このアニメーションに切り替えてしまうのは不自然です。「歩きから斬り掛かる」というアニメージョンデータも用意すればスムーズですが、右足が前に出ているのか、左足が前に出ているのか、それともその間のどこかなのか、歩いているタイミングによって開始の姿勢が異なります。これに対応するには、たくさんのパターンのアニメーションデータを用意しなくてはいけなくなってしまいます。

そこで登場するのが「補間」です。「歩きから斬り掛かる」というアニメーションデータは用意しないで、「歩き」と「斬り掛かる」アニメーションデータを補間してスムーズに切り替えるという手法を用いるのです。

というわけで、回転の補間について考えてみます。2つの回転行列 \(R(\vec{a},\ \theta)\) と \(R(\vec{b},\ \phi)\) があったとします。この2つの回転行列を補間して、時刻 \(t=0\) では \(R(\vec{a},\ \theta)\), 時刻 \(t=1\) では \(R(\vec{b},\ \phi)\) になるような、時間によって変化する回転行列 \(Q(t)\) を作りたいとします。 さて、どんな方法があるでしょうか?

一番ダメな方法は行列の線形補間です。つまり、
$$ Q(t) = (1\ – t) R(\vec{a},\ \theta) + t R(\vec{b},\ \phi) $$
とする方法です。なぜダメかと言うと、\(Q(t)\) が回転行列になるとは限らないからです。例えば、\(\theta = 0\)度, \(\phi = 180\)度の場合を考えてみましょう。このとき、\(R(\vec{a},\ \theta)\) は単位行列となり、\(R(\vec{b},\ \phi)\) は軸 \(\vec{b}\) に直交する2つの成分を反転する行列になります。すると、\(t=0.5\) の中間地点では、軸\(\vec{b}\) に平行な成分を残して他はゼロになってしまう行列が得られてしまいます。もしこの行列を腕のアニメーションに適用したら、腕がつぶれて見えなくなってしまいますね。

では次の方法を考えましょう。
$$ Q(t) = R(\vec{b},\ t\phi)\, R(\vec{a},\ (1-t)\theta) $$
というのはどうでしょう? ちゃんと \(Q(0) = R(\vec{a},\ \theta),\ Q(1) = R(\vec{b},\ \phi)\) となるし、\(Q(t)\) は2つの回転行列の合成なので、ちゃんと回転行列になることが保証されます。なんだかすごく良いように思えるのですが、行列をかける順序が気になります。順番を入れ替えて
$$ Q(t) = R(\vec{a},\ (1-t)\theta)\, R(\vec{b},\ t\phi) $$
じゃだめなんでしょうか? どちらも良いはずですが、かけ算の順番によって結果は異なるはずです。つまり、本当は \(Q(0)\) から \(Q(1)\) にかけて最短経路で補間したいのですが、上のように補間するとそうはならず、このような補間を腕のアニメーションに適用したら、剣を振る瞬間に腕がちょっと遠回りをして不自然な動きになってしまう可能性があります。回転をオイラー角で表現してオイラー角を線形補間した場合も同じような問題が起きます。

ではどうすればいいでしょう? 「クォータニオン!」という声が客席から聞こえてきそうですが、今は無視してまた別の方法を考えてみます。

先程の補間では行列のかけ算の順番が問題でした。2つの行列を対称に扱っていなかったのです。では、回転を\(N\)回に分割して、交互に掛けるのはどうでしょう。
$$ Q(t) = \left\{R(\vec{b},\ \frac{t\phi}{N})\, R(\vec{a},\ \frac{(1-t)\theta}{N})\right\}^N $$
これで \(N\) を無限大に持っていけば、かけ算の順番は関係なくなりそうです。

しかしこんなの計算できるでしょうか? 実はできるんです。\(R(\vec{a},\ \theta)\) は \(e^{\theta\vec{a}\cdot\vec{X}}\)と書くことができました。ですので
$$ Q(t) = \{e^{t\frac{\phi}{N}\vec{b}\cdot\vec{X}} e^{(1-t)\frac{\theta}{N}\vec{a}\cdot\vec{X}}\}^N $$
となりますが、\(N\) が無限大になる極限では、
$$ Q(t) = \{e^{t\frac{\phi}{N}\vec{b}\cdot\vec{X} + (1-t)\frac{\theta}{N}\vec{a}\cdot\vec{X}}\}^N = e^{(t\phi\vec{b} + (1-t)\theta\vec{a})\cdot\vec{X}} $$
と等しくなります。

つまり、回転行列を指数関数で表現して、指数部分を線形補間してやるのです。指数部分はただの足し算であり可換なので、順番は関係なくなりました。この方法は2つの回転行列を対等に扱っているし、オイラー角とは違い結果が座標系に依存しないという点で優れています。

しかし残念なことに、後で具体例を出して説明しますが、この補間でも最短経路を通る理想的な補間にはなっていないのです。では最短経路を通る理想的な補間とはどんな補間でしょう? 今欲しいのは回転行列 \(R(\vec{a},\ \theta)\) であらわされる姿勢で始まり、別の回転行列 \(R(\vec{b},\ \phi)\) であらわされる姿勢へとスムーズに遷移する回転行列 \(Q(t)\) でした。ですので \(R(\vec{b},\ \phi)\, R(\vec{a},\ {-\theta})\) で得られる回転行列 \(R(\vec{c},\ \alpha)\) を作り、
$$ Q(t) = R(\vec{c},\ t\alpha)\, R(\vec{a},\ \theta) $$
とするのが理想的な補間と言えます。

具体例を出して計算してみましょう。まず \(R(\vec{a},\ \theta)\) として、\(x\) 軸まわりに \(180\) 度回転する行列を考えます。
$$ R(\vec{a},\ \theta) = \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1\end{array} \right) $$
そしてもう一つの回転行列 \(R(\vec{b},\ \phi)\) を \(y\) 軸まわりに \(180\) 度回転する行列とします。
$$ R(\vec{b},\ \phi) = \left(\begin{array}{ccc} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1\end{array} \right) $$
すると \(R(\vec{c}, \alpha)\) は \(z\) 軸まわりに180度回転する行列になります。
$$ R(\vec{c}, \alpha) = R(\vec{b},\ \phi)\, R(\vec{a},\ {-\theta}) = \left(\begin{array}{ccc} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1\end{array} \right) $$
つまり、\(R(\vec{a},\ \theta)\) であらわされる姿勢から \(R(\vec{b},\ \phi)\) であらわされる姿勢に遷移するには、\(z\) 軸まわりに \(180\) 度回転すればいいということです。

ちょっとスマホを手に持ってやってみましょう。スマホを横向きに両手で持って画面を正面に向けた状態を初期状態とします。また、ホームボタンは右手側にあるとします。
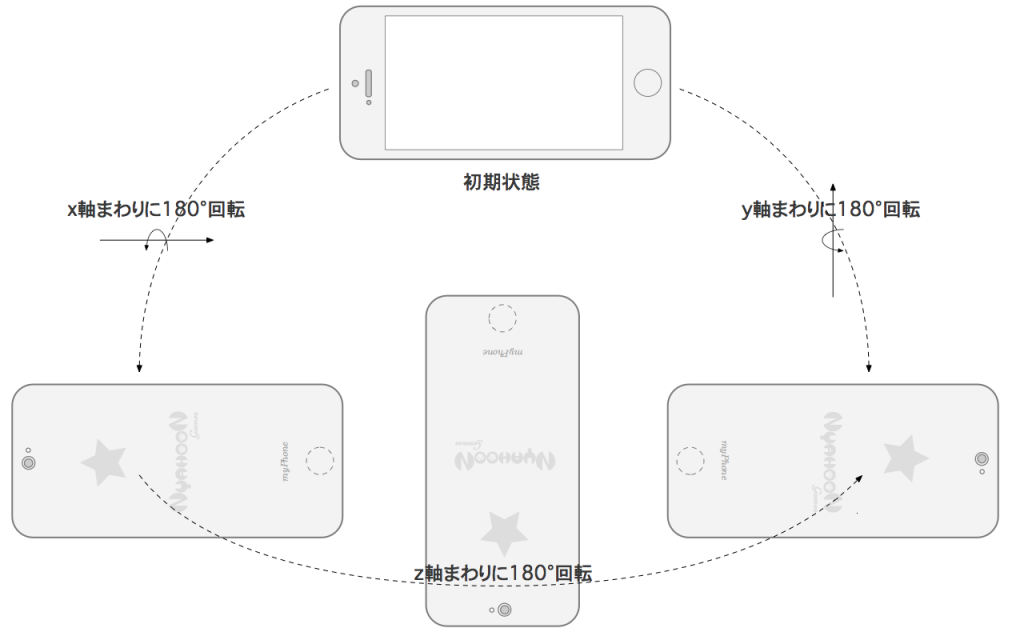さあ、\(x\) 軸まわりに \(180\) 度回転します。ここで \(x\) 軸は左右方向の軸とします。するとスマホの背面が見える状態になりますね。ホームボタンはまだ右手側です。

では初期状態に戻して、今度は \(y\) 軸まわりに \(180\) 度回転します。\(y\) 軸は上下方向の軸とします。すると同じようにスマホの背面が見えますが、今度はホームボタンが左側に来てますね。

さっきの \(x\) 軸まわりに \(180\) 度回転した状態から、今の \(y\) 軸まわりに \(180\) 度回転させた状態に移すとした場合、あなたならどう回転させますか? やっぱり \(z\) 軸(前後方向)まわりに \(180\) 度回転させますよね。

ここで、\(t = 0.5\) のときを考えてみます。理想的な補間では \(Q(t)\) は \(45\) 度ななめ右上方向( \(x\) 軸と \(y\) 軸の中間)を軸として \(180\) 度回転する行列となります。これによって、スマホは初期状態から背面を向けて逆立ちした状態になりますね。

では指数関数表現の指数部分を線形補間した場合はどうでしょう。やはり回転軸は \(x\) 軸と \(y\) 軸の中間を向くわけですが、回転角がちょっと違います。回転角は \(\frac{180}{\sqrt{2}}\) 度となり、これでは回転角が足りません。指数関数表現の指数部分を線形補間する方法では、回転角と回転軸をかけあわせたベクトルを線形補間していたのですが、理想的な補間では角度と回転軸を別々に補間する必要がありそうです。

さて、前置きが長くなりましたが、いよいよクォータニオンの補間について考えてみます。クォータニオンを使えば理想的な補間を簡単に計算できそうです。というのも、クォータニオンなら \(R(\vec{b},\ \phi)\,R(\vec{a}, {-\theta})\) で得られる回転から、回転軸 \(\vec{c}\) と回転角 \(\alpha\) を取り出すのが簡単だからです。

補間するべき2つのクォータニオンを \(q_A,\ q_B\) とします。このとき \(R(\vec{c},\ \alpha) = R(\vec{b},\ \phi)\,R(\vec{a}, {-\theta})\) に対応したクォータニオン \(q_C\) は
$$ q_C = q_B \overline{q_A} $$
で計算できます。\(q_C\) から回転軸 \(\vec{c}\) と回転角 \(\alpha\) を取り出すには、クォータニオンの実数部(スカラー成分)が \(\cos\frac{\alpha}{2}\) になることに着目すればよく、\(q_C\) のスカラー成分を計算するとクォータニオンを4次元ベクトルとみなしたときの内積 \(q_A \cdot q_B\) になるので
$$ \cos\frac{\alpha}{2} = q_A \cdot q_B $$
と書けます。

さて、回転軸 \(\vec{c}\) を \(\vec{c} = (c_x,\ c_y,\ c_z)\) と成分表示したとすると、
$$ q_C = q_B \overline{q_A} = \cos\frac{\alpha}{2} + \sin\frac{\alpha}{2}\,(c_x i + c_y j + c_z k) $$
となるはずなので、
$$ c_x i + c_y j + c_z k = \frac{1}{\sin\frac{\alpha}{2}} \left(q_B \overline{q_A}\ -\ \cos\frac{\alpha}{2}\right) $$
と書くことができます。

これで補間された回転行列 \(Q(t)\) に対応するクォータニオン \(q(t)\) を計算できます。ただし、以降の計算では \(\frac{\alpha}{2}\) と書くのがめんどうなので、\(\beta = \frac{\alpha}{2} = \cos^{-1}(q_A \cdot q_B)\) とすることにします。
\begin{eqnarray*}
q(t) & = & \left\{\cos t\beta + \sin t\beta\, (c_x i + c_y j + c_z k) \right\} q_A\\
& = & \cos t\beta\,q_A + \frac{\sin t\beta}{\sin\beta}\,\left(q_B\ -\ \cos\beta\,q_A\right) \tag{★}
\end{eqnarray*}
となります。もう少し整理すると
\begin{eqnarray*}
q(t) & = & \frac{\sin t\beta}{\sin\beta}\,q_B + \frac{\sin\beta \cos t\beta\ -\ \cos\beta \sin t\beta}{\sin\beta}\,q_A\\
& = & \frac{\sin t\beta}{\sin\beta}\,q_B + \frac{\sin (1-t)\beta}{\sin\beta}\,q_A
\end{eqnarray*}
と書くこともできます。

さて、この補間の幾何学的意味を考えてみます。クォータニオンは大きさが1の4次元ベクトルと見ることができます。2つのクォータニアン \(q_A, q_B\) を図であらわすとこんな感じです。

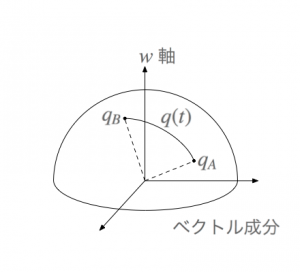
ここで縦軸(\(w\) 軸)はクォータニオンのスカラー成分をあらわし、水平平面はベクトル成分をあらわしています。4次元を図に書くことはできないので、3次元のベクトル成分を2次元平面にまとめています。

この図を、原点および\(q_A,\ q_B\) を通る平面で切って、その断面で2次元の図を書いてみます。クォータニオンの内積 \(q_A \cdot q_B\) が \(\cos\beta\) をあらわしていたので、\(q_A\) と \(q_B\) のなす角は \(\beta\) です。

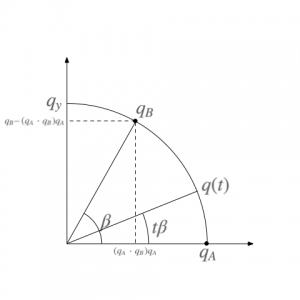
さて、この図の横軸は \(q_A\) ですが、縦軸 \(q_y\) はどうなるでしょう。\(q_A\) と直交して、\(q_A,\ q_B\) と同じ平面上にあるわけだから \(q_B – (q_A \cdot q_B)q_A\) に平行な軸となります。正規化して大きさ1のクォータニオンにすると
\begin{eqnarray}
q_y & = & \frac{q_B – (q_A \cdot q_B)q_A}{|q_B\ – (q_A \cdot q_B)q_A|}\\
& = & \frac{q_B – \cos\beta\,q_A}{\sin\beta}
\end{eqnarray}
となります。

ここで、先程の \(q(t)\) の式で \((★)\) がついている行を見てください。この式は、
$$ (★) = \cos t\beta \, q_A + \sin t\beta \, q_y $$
となっているのがわかると思います。つまり \(q(t)\) は上の図の \(q_A\) とのなす角が \(t\beta\) となる位置のクォータニオンであり、大きさが1の4次元の球面上を \(q_A\) から \(q_B\) に等速で遷移するような補間になっていたのです。このような球面上をまっすぐ等速に補間するものを球面線形補間と呼びます。

補間をする際にひとつ注意点があります。\(q_A\) と \(q_B\) が逆向きだったら、つまり \(q_A \cdot q_B < 0\) だったら、\(\alpha > \pi\ (\beta > \frac{\pi}{2})\) ということになるので、遠まわりな補間になってしまいます。このように補間が遠まわりになってしまうことは、オイラー角を使った場合や指数関数表現を使った場合にも起こりうることで、解決策はどちらかの回転角に \(2\pi\) を足すとか引くとかをすることなのですが、クォータニオンならこの処理は簡単で、\(q_A\) か \(q_B\) のどちらかに負号を付けてやればいいのです(9ページ目の最後を参照)。そうすれば \(-(q_A \cdot q_B) > 0\) となって最短距離の補間となります。

クォータニオンを使うことで、理想的な回転の補間が比較的少ない計算量で求められますようになりました。これが、3Dゲームの開発においてクォータニオンを使う一番大きな理由になります。そうは言っても、\(\cos t\beta\) と \(\sin t\beta\) を計算するために、三角関数と三角関数の逆関数が必要なので、それほど計算が速いわけではありません。もし計算速度を重視するならば、クォータニオンを線形補間してから、それを正規化するという方法もあります。この場合、補間の始まりと終わりのところで \(q(t)\) の変化が少し速くなってしまいますが、理想的な補間と同じ軌道を通ります。また、補間する2つのクォータニオンの間の角度は最大でも90度 (\(q_A \cdot q_B > 0\)) です。最大でも90度の円弧を直線で近似して正規化し直すというのはそんなに悪い近似ではありませんし、線形補間でクォータニオンがゼロになって正規化できなくなる心配もありません(これは行列の線形補間と違うところです)。

こうして見ると、クォータニオンって本当に優秀ですよね。これはクォータニオンが回転行列と同じ積のふるまいを持ちつつ、クォータニオン同士のかけ算がまたクォータニオンになるように都合良く定義したからと言えます。その結果、回転をシンプルな計算で扱えるようになったのです。