クォータニオン徹底解説

2次元の回転と複素数の関係 その1

クォータニアンが発見される前から、複素数で2次元空間の点をあらわすことができ、大きさが1の複素数を掛けることで、原点を中心に点を回転させることができることが知られていました。ここでも、3次元空間の話をする前に2次元空間について考えてみましょう。

複素数は実数と虚数の2つのパラメータを用いて表現されるので、2次元空間上の点として表現することもできます。そしてこの2次元空間を複素平面なんて呼んだりもします。
$$z = x + iy$$
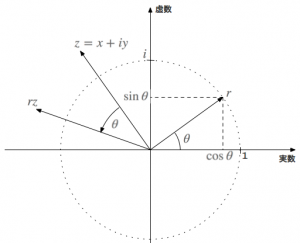
そして不思議なことに、複素数 \(z = x + iy\) に複素平面の単位円上にある別の複素数 \(r = \cos\theta + i\sin\theta\) を掛けてやると
$$ z’ = rz = \cos \theta\,x\ – \sin \theta\,y + i(\sin \theta\,x + \cos \theta\,y) $$
となり、ベクトル \((x,\ y)\) が原点中心に \(\theta\) だけ回転して \( (\cos\theta\,x\ – \sin\theta\,y,\ \sin \theta\,x + \cos \theta\,y)\) に移るのがわかります。

この複素数と回転の関係性はいったいどこからくるのでしょう? これは微小回転について考えると見えてきます。

今、非常に小さい角度 \(\Delta\theta\) だけ2次元空間上の点を原点中心に回転することを考えてみましょう。\(\Delta\theta\) は非常に小さいので \(\Delta\theta ^2\) は無視できるとします。

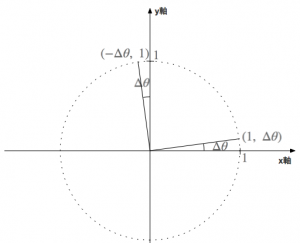
すると、ベクトル \((1,\ 0)\) は \((1,\ \Delta\theta)\), ベクトル \((0,\ 1)\) は \((-\Delta\theta,\ 1)\) へ移動するので、この回転を2×2の行列であらわすと、
\begin{eqnarray*}
\left(\begin{array}{c}x’\\y’\end{array}\right) & = & \left(\begin{array}{cc}1 & -\Delta\theta\\ \Delta\theta & 1 \end{array}\right) \left(\begin{array}{c}x\\y\end{array}\right)\\
& = & \{I + \Delta\theta X\} \left(\begin{array}{c}x\\y\end{array}\right),
\end{eqnarray*}
$$I = \left(\begin{array}{cc}1 & 0\\ 0 & 1 \end{array}\right),\ X = \left(\begin{array}{cc}0 & -1\\ 1 & 0 \end{array}\right) $$
と書けます。微小回転が単位行列 \(I\) と 行列 \(X\) であらわすことができました。さて、この2つの行列をかけ合わせることを考えてみましょう。当然、\(IX = XI = X,\ II = I\) となるわけですが、\(XX\)はどうなるでしょうか? なんと \(XX = -I\) となるではないですか! まさに虚数と同じ性質を持っています。行列 \(X\) を回転の生成子という呼び方をするのですが、回転の生成子と単位行列の組み合わせが、虚数と実数の組み合わせと同じふるまいをするということが2次元空間の回転と複素数の関係性を決めていたのです。

もう少しちゃんと説明すると、2つの行列 \(A, B\) を
\begin{eqnarray*}
A & = & a_x I + a_y X,\\
B & = & b_x I + b_y X
\end{eqnarray*}
として、\(AB\) を計算すると
\begin{eqnarray*}
AB & = & a_x b_x II + a_x b_y IX + a_y b_x XI + a_y b_y XX\\
& = & (a_x b_x – a_y b_y) I + (a_x b_y + a_y b_x) X
\end{eqnarray*}
となるわけですが、これと同じ計算を複素数 \(z_A,\ z_b\)
\begin{eqnarray*}
z_A & = & a_x + i a_y,\\
z_B & = & b_x + i b_y
\end{eqnarray*}
に対して行なえば、同様の結果の
$$ z_Az_B = (a_x b_x – a_y b_y) + i (a_x b_y + a_y b_x) $$
が得られるというわけです。つまり、\(I\) と \(X\) を組み合せたもの(線形結合したもの)は、かけ算において複素数と同じふるまいをするのです。

別の見方をしてみます。回転の生成子 \(X\) は微小回転をあらわしていました。つまり \(X\) を掛けることは回転角 \(\theta\) で微分するようなものです。\(\cos\theta\) を微分すると \(-\sin\theta\) になって、\(\sin\theta\) を微分すると \(\cos\theta\) になりますね。そしてどちらも2回微分すると-1がかかります。だから \(X\) を掛けることは \(x\) と \(y\) を入れ替えること(90度回転)に相当し、\(X\) を2乗すると-1になるのです。そして複素数に \(i\) をかけるのもこれとまったく同じ作用をしているので、複素数が回転と同じ性質を持つわけです。

もっと言ってしまえば、複素数 \(z = x + iy\) に \(i\) をかけると \(iz = -y + ix\) となるので、\(i\) を行列で表現すれば
$$ i = \left(\begin{array}{cc}0 & -1\\ 1 & 0 \end{array}\right) $$
となり、\(X\) と一致するのがわかります。つまり \(i\) と \(X\) は表現方法が違うだけでまったく等価なものと言えます。