クォータニオン徹底解説

3次元の回転とクォータニオン その1

いよいよ3次元の回転とクォータニオンの関係を明らかにしていきます。

2次元の回転行列は複素数と同じふるまいをしました。それは、微小回転によって得られる回転の生成子と虚数 \(i\) が等価なものだったからです(忘れてしまった人は4ページ目を見てください)。それと同じように3次元の回転の生成子とそれに対応する虚数のような何かを見つけるのがおおまかな話の流れになります。

3次元空間の回転は、3次元空間の中で2つの軸を選んで、その2つの軸で構成される2次元平面上での回転と考えることができるので、回転の生成子は2次元の場合と同様に簡単に求まります。例えば、2つの軸として \(x\) 軸と \(y\) 軸を選んだ場合、残りの \(z\) 軸まわりの回転となり、その生成子 \(Z\) は
$$
Z = \left(\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)
$$
となります。
\(x\) 軸まわりの回転の生成子 \(X\), \(\ y\) 軸まわりの回転の生成子 \(Y\) も同様に求まります。
$$
X = \left(\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{array} \right),\
Y = \left(\begin{array}{ccc} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{array} \right)
$$

さて、これら3つの生成子の関係を見てみましょう。\(X, Y, Z\) の2乗は2次元のように単位行列 \(I\) とはなりませんが、回転の影響を受ける2次元の部分空間上では単位行列となり、残りの次元では \(0\) となります。また、3乗すると負号がついて自分自身に戻ります。
$$
X^2 = -\left(\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right),\
Y^2 = -\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right),\
Z^2 = -\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right),\\
X^3 = -X,\ Y^3 = -Y,\ Z^3 = -Z
$$
また、
$$ XY\ – YX = Z,\ YZ\ – ZY = X,\ ZX\ – XZ = Y $$
という関係も成り立つのがわかります。このかけ算の順番を入れ替えて引き算をしたものを交換子と呼んで
$$[X,\ Y] \equiv XY\ – YX$$
というふうに書きます。3つの生成子のうち2つを選んで交換子を作ると残りのもうひとつの生成子になるというのが、3次元空間での回転の重要な特徴となります。
$$ [X,\ Y] = Z,\ [Y,\ Z] = X,\ [Z,\ X] = Y $$

この関係は、\(x\) 軸と \(y\) 軸まわりの回転から \(z\) 軸まわりの回転が発生するというようなことを意味しています。例えば、\(x\) 軸まわりで90度の回転を考えてみましょう。この回転によって、回転後の \(y\) 軸は回転前の \(z\) 軸の位置へ、回転後の \(z\) 軸は \(-y\) 軸の位置へと移動します。ですので、この回転に続いて \(y\) 軸で回転することは、回転前の \(z\) 軸で回転することに相当し、\(z\) 軸で回転することは回転前の \(y\) 軸で逆回転することに相当することになります。

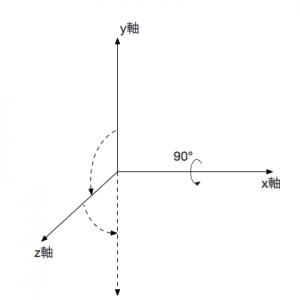
重要なのでちゃんと式で確認してみましょう。今度は微小回転について考えます。\(x\) 軸まわりに \(\Delta\theta\) だけ回転することによって、\(y\) 軸がほんの少し \(z\) 軸側に傾くので、続いて \(y\) 軸まわりに \(\Delta\theta\) だけ回転すると、わずかに \(z\) 軸まわりの回転が発生するはずです。このわずかな回転を取り出すために、さらに \(x\) 軸まわりに \(-\Delta\theta,\ y\) 軸まわりにも \(-\Delta\theta\) を回転させて、微小回転をくるっとひとまわりさせます。これによって \(\Delta\theta\) の1次の項がキャンセルされることになるので、微小回転も2次の項まで考慮すると (2次の項に \(\frac{1}{2}\) がかかるのは前のページ参照)、
\begin{eqnarray*}
& & (I\ – \Delta\theta\, Y + \frac{\Delta\theta^2}{2} Y^2)(I\ – \Delta\theta\, X + \frac{\Delta\theta^2}{2} X^2)(I + \Delta\theta\ Y + \frac{\Delta\theta^2}{2} Y^2)(I + \Delta\theta\ X + \frac{\Delta\theta^2}{2} X^2) \\ & \simeq & I\ – \Delta\theta^2\,[X,\ Y] \\
& = & I\ – \Delta\theta^2\, Z
\end{eqnarray*}
となって、\(x\) 軸まわりの回転と \(y\) 軸まわりの回転を合成すると \(z\) 軸まわりの回転が発生するのがわかります。このように、生成子 \(X,\ Y,\ Z\) の交換関係は3次元空間の回転を合成したときの性質を示しているのです。

ところで、任意軸まわりの微小回転はどう表現できるでしょう? 回転行列は転置すると逆行列になるという性質があります(2ページ目最後の(※)参照)。また、回転行列は回転角が \(0\) なら単位行列になるので、微小回転の行列は単位行列のまわりで \(I + \Delta\theta X_A\) のように書けるはずです。そして、転置すると逆行列になる(\(-\Delta\theta\) の回転になる)ことから、\(X_A^T = -X_A\) でなければいけません。ということは、\(X_A\) の対角成分は \(0\) であり、残りの6つの成分は3つのパラメータで
$$ X_A = \left(\begin{array}{ccc} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{array}\right) $$
と書けるはずですが、これは 生成子 \(X,\ Y,\ Z\) を使って
$$ X_A = a_x X + a_y Y + a_z Z $$
と書けます。つまり、どんな回転軸の微小回転でも生成子 \(X,\ Y,\ Z\) を使って行列を作ることができることがわかります。

さて、2次元の回転のときと同じように、この微小回転の \(\Delta\theta\) を徐々に大きくして任意の角度 \(\theta\) に発展させたとき、回転行列 \(R(\theta)\) は
$$ \frac{d R(\theta)}{d\theta} = X_A R(\theta) $$
という微分方程式を満たすので、
$$ R(\theta) = 1 + \theta X_A + \cdots + \frac{1}{n!}\theta^n {X_A}^n + \cdots $$
とテイラー展開されます。これを計算するには
$$ {X_A}^n = (a_x X + a_y Y + a_z Z)^n $$
を計算する必要があるので、回転の生成子をかけ合わせたときの関係を整理してみましょう。

生成子 \(X, Y, Z\) の間には上記の交換関係の他に
$$
X^3 = -X,\ Y^3 = -Y,\ Z^3 = -Z,
$$
という関係が成り立ちますが、残念なことに \(X^2 = -I\) とはなりません。また \(XY\) や \(YZ,\ ZX\) といった2つの生成子を掛けただけのものも \(I,\ X,\ Y,\ Z\) であらわすことができません。つまり、テイラー展開で任意の回転角を持つ行列を求めると、\(I,\ X,\ Y,\ Z\) の組み合わせでは表現できない行列ができあがります。これは2次元の場合と決定的に異なります。2次元の場合、\(I\) と \(X\) を組み合せたもの同士を掛けても、それはまた \(I\) と \(X\) の組み合わせで表現できました。これは複素数と複素数を掛けたものがまた複素数になるということにも対応しています。

3次元空間の回転に対応したクォータニオンを作ろうとした場合、やはりクォータニオンとクォータニオンを掛けたものがクォータニオンになって欲しいのです。そうでなければクォータニオンを作る意味はなくなってしまいます。ところが、\(I,\ X,\ Y,\ Z\) の組み合わせ(線形結合)ではこの条件を満たすことはできません。

じゃあ、どうするのかというと、でっちあげるのです。「導出するんじゃなくてでっちあげるんかい!」とつっこみを入れたくなる方もいらっしゃるかと思いますが、3次元の回転行列がそのままクォータニオンになるわけではないからこそ、クォータニオンの存在意義があるのです。それに、今までの議論がまったく無駄になるわけではありません。回転を合成したときのふるまいを特徴づける \([X,\ Y] = Z\) という交換関係が重要になってきます。