クォータニオン徹底解説

クォータニオンを使ってベクトルを回転する

前のページまでで、回転行列の積をクォータニオンを使って計算してもよいことを見てきました。しかし、このままではベクトルを回転させるにはクォータニオンを行列の表現に戻さなくてはいけません。どうすればクォータニオンをそのまま使って3次元のベクトルを回転させることができるでしょうか?

2次元のときは回転行列を簡単に2次元ベクトルに写像することができたのですが、3次元ではそうはいきません。しかし、実は3次元の回転行列の中には3次元ベクトルが隠れているのです。それは回転軸です。

というわけで、回転行列を
$$ R(\vec{a},\ \theta) = e^{\theta\, \vec{a} \cdot \vec{X}},\ |\vec{a}| = 1 $$
と書いたときに、\(\vec{a}\) が回転軸になっていることを確認しましょう。

この回転行列を使って任意のベクトル \(\vec{v}\) を回転させると
$$ R(\vec{a},\ \theta)\, \vec{v} = \vec{v} + \theta\, (\vec{a} \cdot \vec{X})\, \vec{v} + \cdots + \frac{\theta^n}{n!}(\vec{a} \cdot \vec{X})^n\, \vec{v} + \cdots $$
とテイラー展開されます。ここで、\(X,\ Y,\ Z\) の定義
$$
X = \left(\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{array} \right),\
Y = \left(\begin{array}{ccc} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{array} \right),\
Z = \left(\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)
$$
から、
$$
\vec{a} \cdot \vec{X} \equiv a_x X + a_y Y + a_z Z = \left(\begin{array}{ccc} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{array} \right)
$$
となり、
$$
(\vec{a} \cdot \vec{X})\, \vec{v} = \vec{a} \times \vec{v}
$$
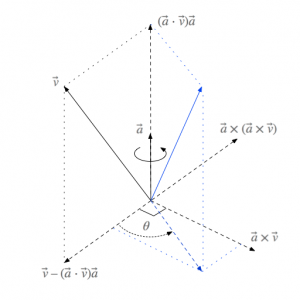
となることがわかります。\(\vec{a} \times \vec{v}\) というのは、ベクトル \(\vec{v}\) のうち \(\vec{a}\) と直交する部分を取り出して、それを \(\vec{a}\) 軸まわりに90度回転させたものになります(下図参照)。そして、もし \(\vec{v}\) が \(\vec{a}\) と平行ならばゼロベクトルになって、ベクトル \(\vec{v}\) は回転の影響を受けなくなります。これだけで \(\vec{a} \cdot \vec{X}\) が 回転軸 \(\vec{a}\) まわりの回転の生成子になっていそうなことがわかるわけですが、ちゃんと最後まで計算してみましょう。

\((\vec{a} \cdot \vec{X})^2\, \vec{v}\) を計算すると
\begin{eqnarray*}
(\vec{a} \cdot \vec{X})^2\, \vec{v} & = & \vec{a} \times (\vec{a} \times \vec{v})\\
& = & (\vec{a}\cdot\vec{v})\,\vec{a}\ – (\vec{a}\cdot\vec{a})\,\vec{v}\\
& = & \ – (\vec{v}\ – (\vec{a}\cdot\vec{v})\,\vec{a})
\end{eqnarray*}
となります。この式の変形になじみのない人もいるかもしれませんが、\(\vec{a} \times (\vec{a} \times \vec{v})\) は \(\vec{a} \times \vec{v}\) を \(\vec{a}\) 軸まわりに90度回転させたものであることに気づけば理解できると思います(下図参照)。そして、\(\vec{v}\ – (\vec{a}\cdot\vec{v})\,\vec{a}\) はベクトル \(\vec{v}\) のうち、\(\vec{a}\) と直交する成分になっていることにも注意してください。

さて、\((\vec{a} \cdot \vec{X})^3\, \vec{v}\) はどうなるでしょう?
\begin{eqnarray*}
(\vec{a} \cdot \vec{X})^3\, \vec{v} & = & \vec{a} \times ((\vec{a} \cdot \vec{X})^2\, \vec{v})\\
& = & – \vec{a} \times (\vec{v}\ – (\vec{a}\cdot\vec{v})\,\vec{a})\\
& = & \ – \vec{a}\cdot\vec{v}
\end{eqnarray*}
\((\vec{a} \cdot \vec{X})\, \vec{v}\) に負号がついたものになりましたね。

ここまでくれば \((\vec{a} \cdot \vec{X})^n\, \vec{v}\) も計算できます。
$$
(\vec{a} \cdot \vec{X})^n\, \vec{v} = \left\{ \begin{split}
& (-1)^\frac{n}{2} (\vec{v}\ – (\vec{a}\cdot\vec{v})\,\vec{a}) & \ \ (n が偶数のとき)\\
& (-1)^\frac{n – 1}{2} \vec{a} \times \vec{v} & \ \ (n が奇数のとき) \end{split} \right.
$$

以上から、
\begin{eqnarray*}
R(\vec{a},\ \theta)\, v & = & (\vec{a}\cdot\vec{v})\,\vec{a} + \left\{1\ – \frac{\theta^2}{2!} + \cdots + (-1)^n \frac{\theta^{2n}}{(2n)!} + \cdots \right\} (\vec{v}\ – (\vec{a}\cdot\vec{v})\,\vec{a})\\
& & \ + \left\{\theta + \cdots + (-1)^n \frac{\theta^{2n + 1}}{(2n+1)!} + \cdots \right\} \vec{a} \times \vec{v}\\
& = & (\vec{a} \cdot \vec{v})\, \vec{a} + \cos\theta\, (\vec{v}\ – (\vec{a} \cdot \vec{v})) + \sin\theta\, \vec{a} \times \vec{v}
\end{eqnarray*}
となります。さっきから同じようなテイラー展開によって \(\sin,\ \cos\) が出てきてますね。これは2乗すると \(-1\) になる(あるいは3乗すると負号がついて自分自身に戻る)という性質に由来するもので、この性質が回転をあらわしていると言えます。

さて、上の図を見ながら、この式の各項のベクトルに注目してみましょう。第1項はベクトル \(\vec{v}\) のうち、\(\vec{a}\) に平行な成分をあらわしていて、回転の影響を受けません。そして第2項の \(\cos\theta\) がかかったベクトルはベクトル \(\vec{v}\) のうち、\(\vec{a}\) に直交する成分をあらわしています。そして第3項の \(\sin\theta\) がかかった項は上記2つのベクトルと直交し、大きさが第2項のベクトルと同じものをあらわしています。まさに、ベクトル \(\vec{v}\) が回転軸 \(\vec{a}\) のまわりに角度 \(\theta\) だけ回転しているのがわかりますね。

ちょっと長くなってしまいましたが、これで回転行列 \(R(\vec{a},\ \theta)\) の \(\vec{a}\) が回転軸をあらわし、\(\theta\) が回転角をあらわしていることがわかりました。ですので、\(R(\vec{a},\ \theta)\) を別の回転行列で座標変換すれば、\(\vec{a}\) を座標変換した回転軸を持つ回転行列が得られるはずです。でも行列の座標変換とはどうすればよいのでしょう?

ある回転行列 \(A\) があり、ベクトル \(\vec{x}\) がベクトル \(\vec{y}\) に移るとします。
$$ \vec{y} = A\, \vec{x} $$
さて、別の回転行列 \(R\) で \(\vec{x},\ \vec{y}\) が \(\vec{x}’,\ \vec{y}’\) に変換されるとすると、
\begin{eqnarray*}
\vec{x}’ & = & R\,\vec{x},\\
\vec{y}’ & = & R\,\vec{y}\\
& = & RA\,\vec{x} = (RAR^{-1})R\vec{x} = A’\vec{x}’,\\
A’ & = & RAR^{-1}
\end{eqnarray*}
と書けます。行列 \(A’ = RAR^{-1}\) が座標変換後のベクトル \(\vec{x}’\) を回転させて \(\vec{y}’\) に移していますね。つまり、行列 \(A\) を \(R\) で座標変換すると \(RAR^{-1}\) となるわけです。そして、\(RAR^{-1}\) が持つ回転軸は、\(A\) が持つ回転軸を行列 \(R\) で回転させたものになっているはずです。

これでクォータニオンを使ってベクトルを回転することができます。我々はすでに回転行列のかけ算とクォータニオンのかけ算が同じふるまいをすることを知っています。ある回転行列に対応したクォータニオン \(q\) が次のように書けるとしましょう。
$$ q = (w,\ \vec{v}) \equiv w + v_x i + v_y j + v_z k $$
ここでは、クォータニオンをスカラー成分 \(w\) とベクトル成分 \(\vec{v}\) を使って \((w,\ \vec{v})\) と表記することにします。このとき、\(\vec{v}\) はこの回転の回転軸に平行なベクトルとなっているはずです。これを別の回転行列に対応した クォータニオン \(r\) を使って
$$ q’ = rqr^{-1} $$
を計算すれば、ベクトル \(\vec{v}\) をクォータニオン \(r\) で回転した結果を \(q’\) のベクトル成分から得ることができるはずです。

実際に計算して確かめてみましょう。
$$ r = \left(\cos\frac{\theta}{2},\ \sin\frac{\theta}{2}\, \vec{a}\right) $$
とすれば、逆回転の \(r^{-1}\) は回転角を \(-\theta\) とすれば得られるので、
$$ r^{-1} = \overline{r} = \left(\cos\frac{\theta}{2},\ {-\sin\frac{\theta}{2}}\, \vec{a}\right) $$
となります。よって、
\begin{eqnarray*}
q’ & = & rq\overline{r}\\
& = & \left(\cos\frac{\theta}{2},\ \sin\frac{\theta}{2}\,\ \vec{a}\right) (w,\ \vec{v}) \left(\cos\frac{\theta}{2},\ -\sin\frac{\theta}{2}\, \vec{a}\right) \\
& = & \left(w \cos\frac{\theta}{2}\ – \sin\frac{\theta}{2}\,\ \vec{a} \cdot \vec{v},\ \cos\frac{\theta}{2}\, \vec{v} + w \sin\frac{\theta}{2}\, \vec{a} + \sin\frac{\theta}{2}\, \vec{a} \times \vec{v}\right) \left(\cos\frac{\theta}{2},\ -\sin\frac{\theta}{2}\, \vec{a}\right) \\
& = & \left(w \cos^2\frac{\theta}{2}\ + w \sin^2\frac{\theta}{2},\ \sin^2\frac{\theta}{2}\, (\vec{a}\cdot\vec{v})\, \vec{a} + \cos^2\frac{\theta}{2}\, \vec{v} \ + 2 \sin\frac{\theta}{2} \cos\frac{\theta}{2}\,\vec{a} \times \vec{v}\ – \sin^2\frac{\theta}{2}\, (\vec{a}\times\vec{v})\times \vec{a}\right)\\
& = & \left(w,\ (\vec{a}\cdot\vec{v})\, \vec{a} + \left(\cos^2\frac{\theta}{2}\ – \sin^2\frac{\theta}{2}\right) \vec{v} + 2 \sin\frac{\theta}{2} \cos\frac{\theta}{2}\,\vec{a} \times \vec{v}\ + 2 \sin^2\frac{\theta}{2}\, (\vec{a}\cdot\vec{v})\, \vec{a}\ \right) \\
& = & \left(w,\ (\vec{a}\cdot\vec{v})\, \vec{a} + \cos\theta\, (\vec{v}\ – (\vec{a}\cdot\vec{v})\, \vec{a}) + \sin\theta\, \vec{a} \times \vec{v} \right)
\end{eqnarray*}
が得られ、ちゃんと \(\vec{v}\) が回転軸 \(\vec{a}\) のまわりに角度 \(\theta\) だけ回転されているのが確認できます。ここでも最後から2番目の式変形で
$$ (\vec{a}\times\vec{v})\times \vec{a} = -\vec{a} \times (\vec{a}\times\vec{v}) = \vec{v}\ – (\vec{a}\cdot\vec{v})\, \vec{a} $$
を使い、最後の式変形では三角関数の倍角の公式
$$
\cos^2\frac{\theta}{2}\ – \sin^2\frac{\theta}{2} = 1\ – 2 \sin^2\frac{\theta}{2} = \cos\theta,\\
2\sin\frac{\theta}{2} \cos\frac{\theta}{2} = \sin\theta
$$
を使いました。単にクォータニオンを天下り的に教えられただけの人にとってはまるで魔法みたいな結果ですが、行列のかけ算とクォータニオンのかけ算が同じふるまいをすることを知った我々にとって、これはなるべくしてなった当然の結果と言えます。

念の為補足しておくと、クォータニオン \(q\) を回転をあらわすクォータニオンとしていましたが、これを任意のクォータニオンとしてもかまいません。なぜなら、\(q’ = rq \overline{r}\) という式は両辺をスカラー倍しても成り立つわけですが、任意のクォータニオン \(q = (w,\ \vec{v})\) に対して大きさが1のクォータニオン
$$ \frac{q}{|q|} = \left(\frac{w}{|q|},\ \frac{|\vec{v}|}{|q|}\frac{\vec{v}}{|v|}\right),\ |q| = \sqrt{w^2 + |\vec{v}|^2} $$
を作ると、それは回転軸を \(\frac{\vec{v}}{|\vec{v}|}\) とし、回転角 \(\theta\) が
\begin{eqnarray*}
\cos\frac{\theta}{2} & = & \frac{w}{|q|},\\
\sin\frac{\theta}{2} & = & \sqrt{1 – \cos^2\frac{\theta}{2}} = \frac{|\vec{v}|}{|q|}
\end{eqnarray*}
となる回転をあらわすクォータニオンになるので、これを別の回転をあらわすクォータニオン \(r\) で回転させた式
$$ \frac{q’}{|q|} = r\frac{q}{|q|} \overline{r} $$
の両辺に \(|q|\) をかけることによって、任意のクォータニオンに対する式、
$$ q’ = rq \overline{r} $$
を得ることができるからです。

特に、3次元ベクトルを回転させる目的ならば \(w = 0\) とした方が計算が楽なので、任意のベクトル \(\vec{v}\) に対して
$$ (0,\ \vec{v’}) = r\, (0,\ \vec{v})\, \overline{r} $$
で回転されたベクトル \(\vec{v}’\) を計算することができます。