さて、計算が終わったので、シェーダーを実装して結果をライトマップに焼き込んだものと比べてみましょう。
シェーダーコードはこちら。関数の引数の p はライトローカル座標系での位置、n が法線ベクトル、areaSizeAndHalfSize は xy 成分がエリアライトの縦横のサイズ、zw 成分がサイズを2で割ったもので、関数の戻り値が前のページでの積分結果 \(\frac{2I}{L_0}\) を返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
float AreaLightDiffuse(float3 p, float3 n, float4 areaSizeAndHalfSize) { if (p.z < 0) { return 0; } // n.x, n.y が 0 以上になるように座標系を反転させる. float2 s = 2.0f * step(0, n.xy) - 1; p.xy *= s; n.xy *= s; float4 x = -p.xyxy; x.xy -= areaSizeAndHalfSize.zw; x.zw += areaSizeAndHalfSize.zw; // 各ケースごとに場合分け. float3 Dn = p.z * n; float N11 = dot(n.xy, x.zw) - Dn.z; if (N11 < 0) { // 前のページの最初のケース. return 0; } else { // 点 p を通り法線が n の平面がエリアライトと交差するときに、エリアを左右ではなく上下に分割するように // (前のページのx'_0 = x_0, x'_1 = x_1 のケースになるように) x 軸と y 軸を入れ替える. float2 d = n.x * x.xz + n.y * x.wy; if (d.x < d.y) { x = x.yxwz; n.xy = n.yx; d.xy = d.yx; Dn.xy = Dn.yx; areaSizeAndHalfSize.xy = areaSizeAndHalfSize.yx; } float D2 = p.z*p.z; float2 D2x11 = D2 + x.zw*x.zw; float2 R11 = rsqrt(D2x11); float2 X11 = Dn.xy + n.z * x.zw; float2 A11 = X11*R11; float2 N01 = d - Dn.z; if (N01.x <= 0) { float D2_11 = D2 + dot(x.zw, x.zw); // 前のページの5番目(最後から2番目)のケース. float I = atan2(p.z*N11, X11.x*X11.y - x.z*x.w); I -= A11.y * atan2(N11, R11.y*(n.x*D2_11 - N11 * x.z)); I -= A11.x * atan2(N11, R11.x*(n.y*D2_11 - N11 * x.w)); return I; } else { float I = A11.y * atan2(areaSizeAndHalfSize.x, R11.y*(D2x11.y + x.x*x.z)); if (N01.y <= 0) { // 前のページの3番目のケース. float ny1 = n.y*x.w; float Y1 = Dn.z - n.x * x.z; float N11 = ny1 - Y1; I += A11.x * atan2(N11, R11.x*(n.y*D2x11.x + Y1*x.w)); float Dx0 = D2 + x.x*x.x; float Rx0 = rsqrt(Dx0); float2 XX01 = Dn.xx + n.z * x.xz; float Ax0 = XX01.x*Rx0; float Y0 = Dn.z - n.x * x.x; float N01 = ny1 - Y0; I = Ax0 * atan2(N01, Rx0*(n.y*Dx0 + Y0*x.w)) - I; I += atan2(Dn.y*areaSizeAndHalfSize.x, D2 + x.x*x.z - XX01.x*XX01.y); } else { I += A11.x * atan2(areaSizeAndHalfSize.y, R11.x*(D2x11.x + x.y*x.w)); float2 D2x00 = D2 + x.xy*x.xy; float2 R00 = rsqrt(D2x00); float2 X00 = Dn.xy + n.z * x.xy; float2 A00 = X00*R00; if (dot(x.xy, n.xy) - Dn.z < 0) { // 前のページの6番目(最後)のケース. I += atan2(p.z*(dot(n.xy, x.xy) - Dn.z), X00.x*X00.y - x.x*x.y); I = A00.x * atan2(N01.x, R00.x*(n.y*D2x00.x + (Dn.z - n.x*x.x)*x.w)) - I; I += A00.y * atan2(N01.y, R00.y*(n.x*D2x00.y + (Dn.z - n.y*x.y)*x.z)); } else { // 前のページの2番目(エリア全体)のケース. I = A00.x * atan2(areaSizeAndHalfSize.y, R00.x*(D2x00.x + x.y*x.w)) - I; I += A00.y * atan2(areaSizeAndHalfSize.x, R00.y*(D2x00.y + x.x*x.z)); } } return I; } } } |
さて、上記の関数は前のページの \(\frac{2I}{L_0}\) を返します。エリアライト上の点光源が角度\(\theta\)方向に放出するライトの強さを \(L_0\cos\theta\) としていたので、Unity のエリアライトが持つ Intensity プロパティは、
\begin{eqnarray*}
L_0\int_{0}^{2\pi}d\phi\int_{0}^{\frac{\pi}{2}}\cos\theta\sin\theta d\theta & = & \pi L_0\left[\sin^2\theta\right]_{0}^{\frac{\pi}{2}} \\
& = & \pi L_0
\end{eqnarray*}
で計算できると考えるのが妥当です。なので、上記関数の戻り値に Intensity\(/2\pi\) を掛けたものをシェーダーの出力とします。
このシェーダーの出力と、Unityでベイクしたエリアライトの結果を比べてみます。
上のシェーダーの全ての分岐がテストされるように、ライトの位置を動かしながら、いくつかスクリーンショットを撮りました。
各画像の左側がシェーダーでレンダリングしたもの、右側がライトマップにベイクしたものです。また、Player Settings で Color Space を Linear に設定しています。
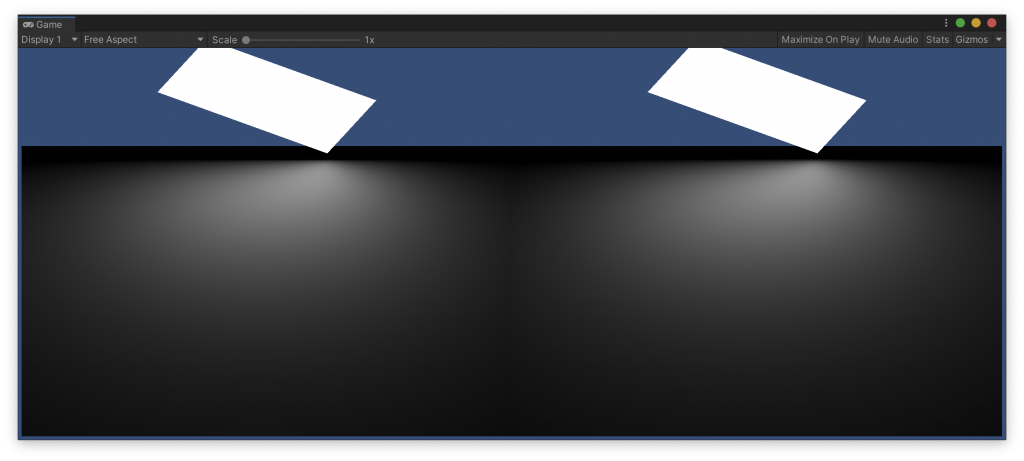
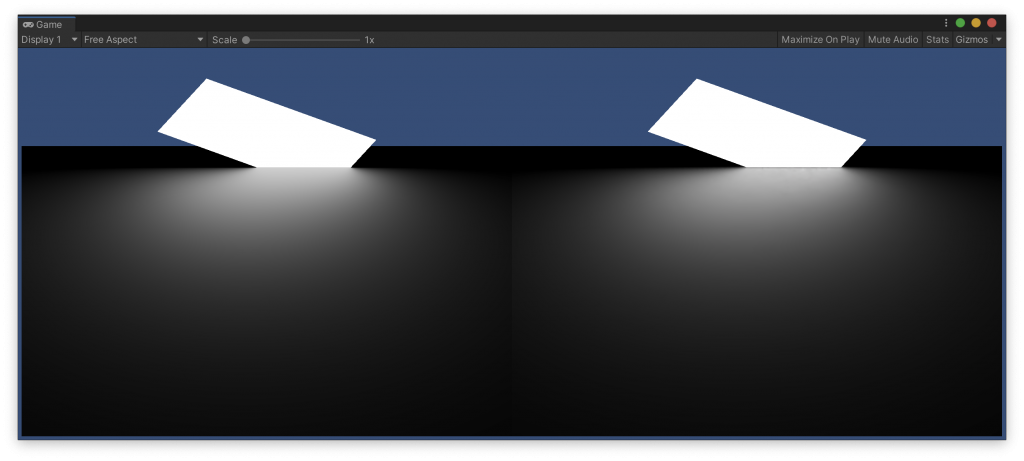
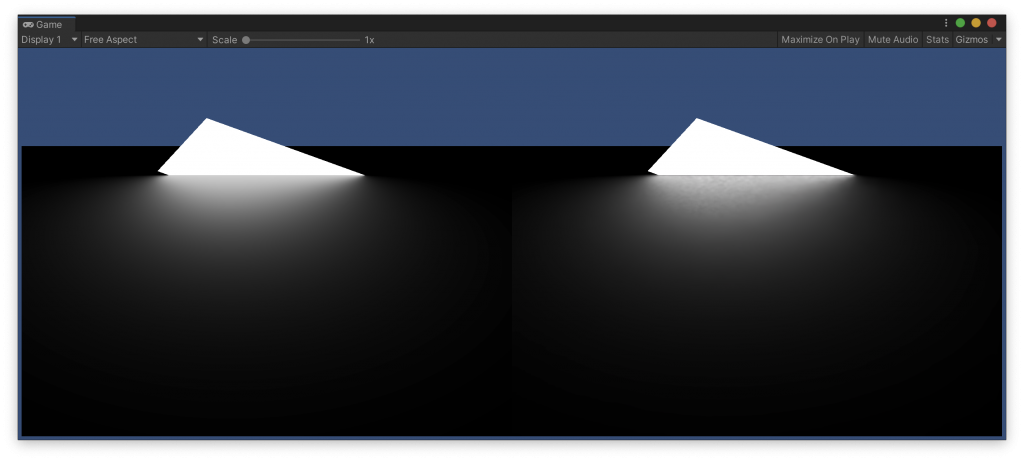
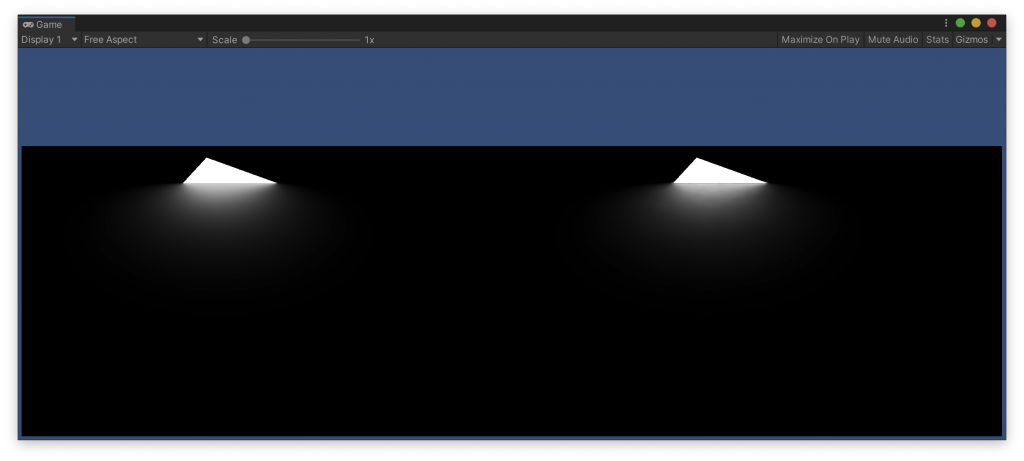
もう、完全に一致していると言っていいレベルじゃないでしょうか。前回は一生懸命計算して違う結果になってしまい、心が折れかけましたが、これは嬉しい。この計算をフラグメントシェーダーで行うのはちょっと気が引けますが、影の濃さを評価するために頂点シェーダーで行うくらいはいいかなと思うので、これを使ってエリアライトの影のプロジェクターを実装してみようと思います。

