すべての積分を計算できたので、つなげてみましょう。
\begin{eqnarray*}
x’_0 & = & max\left(x_0,\ min\left(x_1,\ \frac{Dn_z\ – n_y y_1}{n_x}\right)\right),\\
x’_1 & = & min\left(x_1,\ max\left(x_0,\ \frac{Dn_z\ – n_y y_0}{n_x}\right)\right),\\
y(x) & = & \frac{Dn_z\ – n_x x}{n_y}
\end{eqnarray*}
として、
$$
I = \frac{L_0 D}{2} \int_{x’_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – \frac{L_0 D}{2} \int_{x’_0}^{x’_1}\!\!\! F(x, y(x))\,dx\ – \frac{L_0 D}{2} \int_{x’_1}^{x_1}\!\!\! F(x, y_0)\,dx
$$
と書けたわけですが、前回と同様に場合わけをします。
まずは一番簡単な \(x’_0 = x’_1 = x_1\) の場合。
$$ I = 0 $$
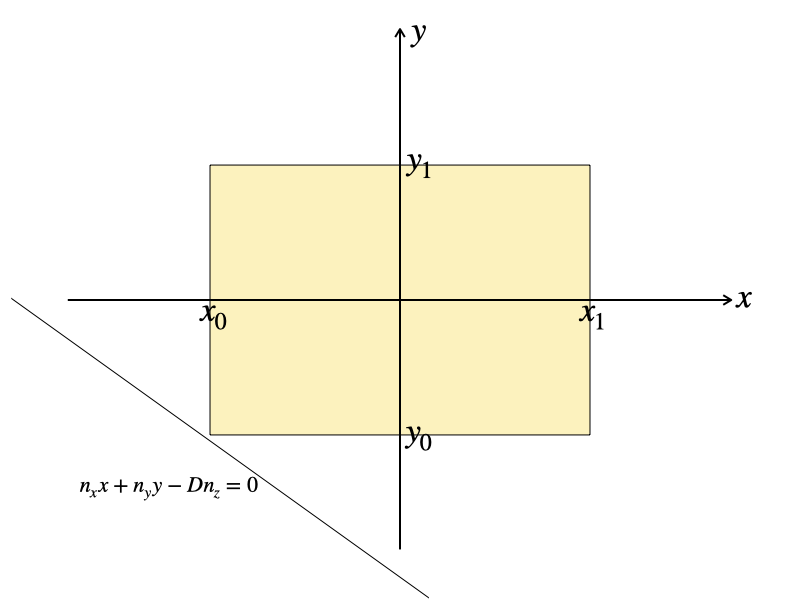
次に簡単なのが、\(x’_0 = x’_1 = x_0\) の場合。積分区間が対象なので、積分結果も \(x\) と \(y\) の入れ替えに対して対象になっています。
\begin{eqnarray*}
\frac{2I}{L_0} & = & D\int_{x_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – D\int_{x_0}^{x_1}\!\!\! F(x, y_0)\,dx \\
& = & \frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{y_1}{\sqrt{D^2+x_0^2}}+\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{x_0}{\sqrt{D^2+y_1^2}} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{y_1}{\sqrt{D^2+x_1^2}}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{x_1}{\sqrt{D^2+y_1^2}} \\
& & {}-\frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{y_0}{\sqrt{D^2+x_0^2}}-\frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{x_0}{\sqrt{D^2+y_0^2}} \\
& & {}+\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{y_0}{\sqrt{D^2+x_1^2}}+\frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{x_1}{\sqrt{D^2+y_0^2}}
\end{eqnarray*}
ここで、\(\tan\) の加法定理から
$$ \tan(\arctan x-\arctan y) = \frac{x-y}{1+xy} $$
となり、
$$ \arctan x-\arctan y = \arctan\frac{x-y}{1+xy} $$
が言えるので、
\begin{eqnarray*}
\frac{2I}{L_0} & = & \frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{\sqrt{D^2+x_0^2}(y_1-y_0)}{D^2+x_0^2+y_0y_1} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{\sqrt{D^2+x_1^2}(y_1-y_0)}{D^2+x_1^2+y_0y_1} \\
& & {}+\frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{\sqrt{D^2+y_0^2}(x_1-x_0)}{D^2+y_0^2+x_0x_1} \\
& & {}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{\sqrt{D^2+y_1^2}(x_1-x_0)}{D^2+y_1^2+x_0x_1}
\end{eqnarray*}
とまとめることができます。
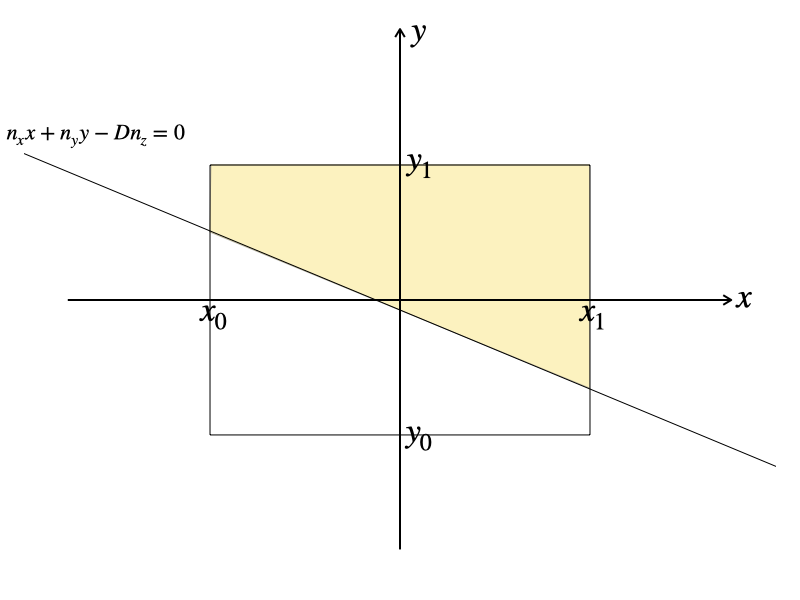
次は \(x’_0 = x_0,\ x’_1 = x_1\) の場合です。
\begin{eqnarray*}
\frac{2I}{L_0} & = & D\int_{x_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – D\int_{x_0}^{x_1}\!\!\! F(x, y(x))\,dx \\
& = & \frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{y_1}{\sqrt{D^2+x_0^2}}+\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{x_0}{\sqrt{D^2+y_1^2}} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{y_1}{\sqrt{D^2+x_1^2}}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{x_1}{\sqrt{D^2+y_1^2}} \\
& & {}-\frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{y(x_0)}{\sqrt{D^2+x_0^2}}-\arctan\frac{n_yx_0-n_xy(x_0)}{D} \\
& & {}+\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{y(x_1)}{\sqrt{D^2+x_1^2}}+\arctan\frac{n_yx_1-n_xy(x_1)}{D} \\
& = & \frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{\sqrt{D^2+x_0^2}(y_1-y(x_0))}{D^2+x_0^2+y(x_0)y_1} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{\sqrt{D^2+x_1^2}(y_1-y(x_1))}{D^2+x_1^2+y(x_1)y_1} \\
& & {}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{\sqrt{D^2+y_1^2}(x_1-x_0)}{D^2+y_1^2+x_0x_1} \\
& & {}+\arctan\frac{D\{n_y(x_1-x_0)+n_x(y(x_0)-y(x_1))\}}{D^2+(n_yx_0-n_xy(x_0))(n_yx_1-n_xy(x_1))} \\
& = & \frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{\sqrt{D^2+x_0^2}(n_xx_0+n_yy_1-Dn_z)}{n_y(D^2+x_0^2)+(Dn_z-n_xx_0)y_1} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{\sqrt{D^2+x_1^2}(n_xx_1+n_yy_1-Dn_z)}{n_y(D^2+x_1^2)+(Dn_z-n_xx_1)y_1} \\
& & {}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{\sqrt{D^2+y_1^2}(x_1-x_0)}{D^2+y_1^2+x_0x_1} \\
& & {}+\arctan\frac{Dn_y(x_1-x_0)}{D^2+x_0x_1-(Dn_x+n_zx_0)(Dn_x+n_zx_1)}
\end{eqnarray*}
次は \(x_0 \le x’_0 \le x’_1 \le x_1\) の場合。
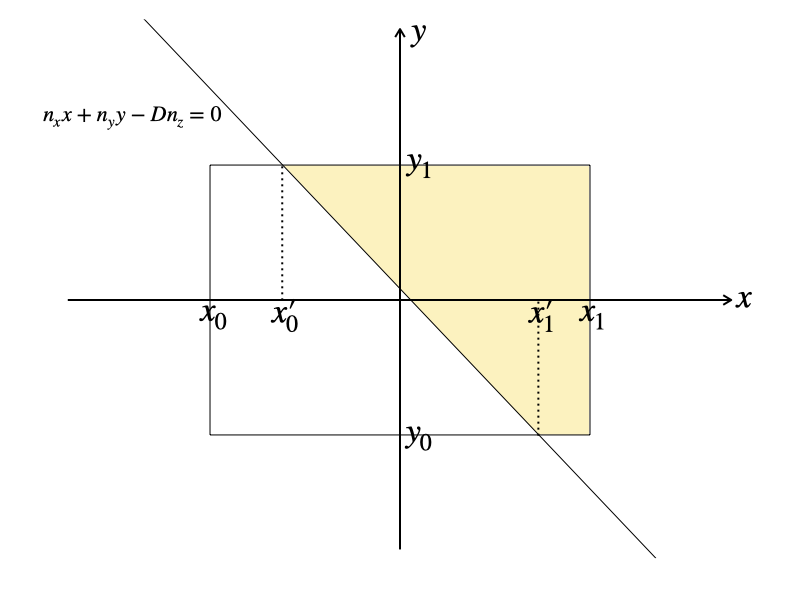
ここで、\(x’_0 = x(y_1),\ x’_1 = x(y_0),\ x(y) = \frac{Dn_z – n_y y}{n_x}\) と書くことにします。
\begin{eqnarray*}
\frac{2I}{L_0} & = & D\int_{x’_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – D\int_{x’_0}^{x’_1}\!\!\! F(x, y(x))\,dx\ – D\int_{x’_1}^{x_1}\!\!\! F(x, y_0)\,dx \\
& = & \frac{Dn_x+n_zx(y_1)}{\sqrt{D^2+x(y_1)^2}}\arctan\frac{y_1}{\sqrt{D^2+x(y_1)^2}}+\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{x(y_1)}{\sqrt{D^2+y_1^2}} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{y_1}{\sqrt{D^2+x_1^2}}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{x_1}{\sqrt{D^2+y_1^2}} \\
& & {}-\frac{Dn_x+n_zx(y_1)}{\sqrt{D^2+x(y_1)^2}}\arctan\frac{y_1}{\sqrt{D^2+x(y_1)^2}}-\arctan\frac{n_yx(y_1)-n_xy_1}{D} \\
& & {}+\frac{Dn_x+n_zx(y_0)}{\sqrt{D^2+x(y_0)^2}}\arctan\frac{y_0}{\sqrt{D^2+x(y_0)^2}}+\arctan\frac{n_yx(y_0)-n_xy_0}{D} \\
& & {}-\frac{Dn_x+n_zx(y_0)}{\sqrt{D^2+x(y_0)^2}}\arctan\frac{y_0}{\sqrt{D^2+x(y_0)^2}}-\frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{x(y_0)}{\sqrt{D^2+y_0^2}} \\
& & {}+\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{y_0}{\sqrt{D^2+x_1^2}}+\frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{x_1}{\sqrt{D^2+y_0^2}} \\
& = & \frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{\sqrt{D^2+y_0^2}(x_1-x(y_0))}{D^2+y_0^2+ x(y_0)x_1} \\
& & {}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{\sqrt{D^2+y_1^2}(x_1-x(y_1))}{D^2+y_1^2+x(y_1)x_1} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{\sqrt{D^2+x_1^2}(y_1-y_0)}{D^2+x_1^2+y_0y_1} \\
& & {}+\arctan\frac{D\{n_y(x(y_0)-x(y_1))+n_x(y_1-y_0)\}}{D^2+(n_yx(y_0)-n_xy_0)(n_yx(y_1)-n_xy_1)} \\
& = & \frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{\sqrt{D^2+y_0^2}(n_xx_1+n_yy_0-Dn_z)}{n_x(D^2+y_0^2)+(Dn_z-n_yy_0)x_1} \\
& & {}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{\sqrt{D^2+y_1^2}(n_xx_1+n_yy_1-Dn_z)}{n_x(D^2+y_1^2)+(Dn_z-n_yy_1)x_1} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{\sqrt{D^2+x_1^2}(y_1-y_0)}{D^2+x_1^2+y_0y_1} \\
& & {}+\arctan\frac{Dn_x(y_1-y_0)}{D^2+y_0y_1-(Dn_y+n_zy_0)(Dn_y+n_zy_1)}
\end{eqnarray*}
さて、前回はこの結果の \(x\) と \(y\) を入れ替えたものが、\(x’_0 = x_0,\ x’_1 = x_1\) の場合の結果と一致しなくて、計算間違いの可能性も捨てきれなかったのですが、今回は見事に一致してくれました。めでたしめでたし。
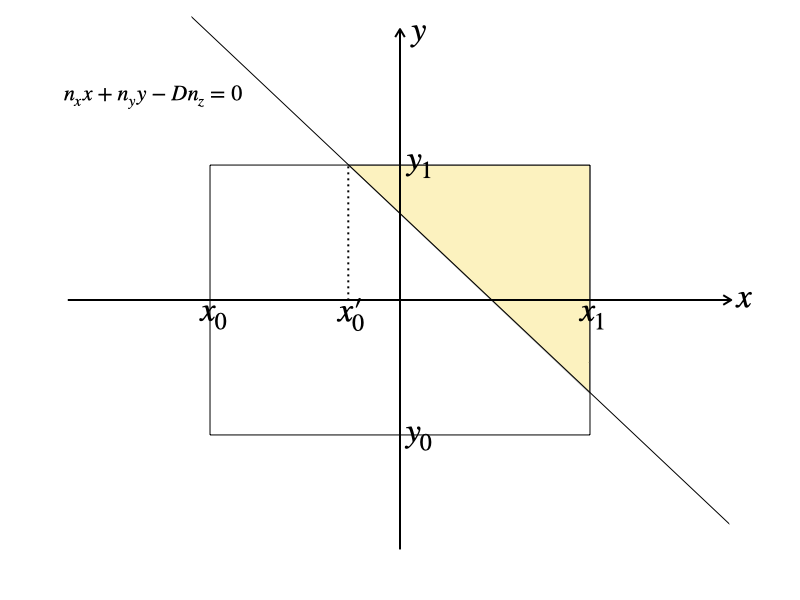
次は \(x_0 \le x’_0 \le x’_1 = x_1\) の場合です。
\begin{eqnarray*}
\frac{2I}{L_0} & = & D\int_{x’_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – D\int_{x’_0}^{x_1}\!\!\! F(x, y(x))\,dx \\
& = & \frac{Dn_x+n_zx(y_1)}{\sqrt{D^2+x(y_1)^2}}\arctan\frac{y_1}{\sqrt{D^2+x(y_1)^2}}+\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{x(y_1)}{\sqrt{D^2+y_1^2}} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{y_1}{\sqrt{D^2+x_1^2}}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{x_1}{\sqrt{D^2+y_1^2}} \\
& & {}-\frac{Dn_x+n_zx(y_1)}{\sqrt{D^2+x(y_1)^2}}\arctan\frac{y_1}{\sqrt{D^2+x(y_1)^2}}-\arctan\frac{n_yx(y_1)-n_xy_1}{D} \\
& & {}+\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{y(x_1)}{\sqrt{D^2+x_1^2}}+\arctan\frac{n_yx_1-n_xy(x_1)}{D} \\
& = & \arctan\frac{D\{n_y(x_1-x(y_1)))+n_x(y_1-y(x_1))\}}{D^2+(n_yx_1-n_xy(x_1))(n_yx(y_1)-n_xy_1)} \\
& & {}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{\sqrt{D^2+y_1^2}(x_1-x(y_1))}{D^2+y_1^2+x(y_1)x_1} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{\sqrt{D^2+x_1^2}(y_1-y(x_1))}{D^2+x_1^2+ y(x_1)y_1} \\
& = & \arctan\frac{D(n_xx_1+n_yy_1-Dn_z)}{(Dn_x+n_zx_1)(Dn_y+n_zy_1)-x_1y_1} \\
& & {}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{\sqrt{D^2+y_1^2}(n_xx_1+n_yy_1-Dn_z)}{n_x(D^2+x_1^2+y_1^2)-(n_xx_1+n_yy_1-Dn_z)x_1} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{\sqrt{D^2+x_1^2}(n_xx_1+n_yy_1-Dn_z)}{n_y(D^2+x_1^2+y_1^2)-(n_xx_1+n_yy_1-Dn_z)y_1}
\end{eqnarray*}
最後に \(x_0 = x’_0 \le x’_1 \le x_1\) の場合。
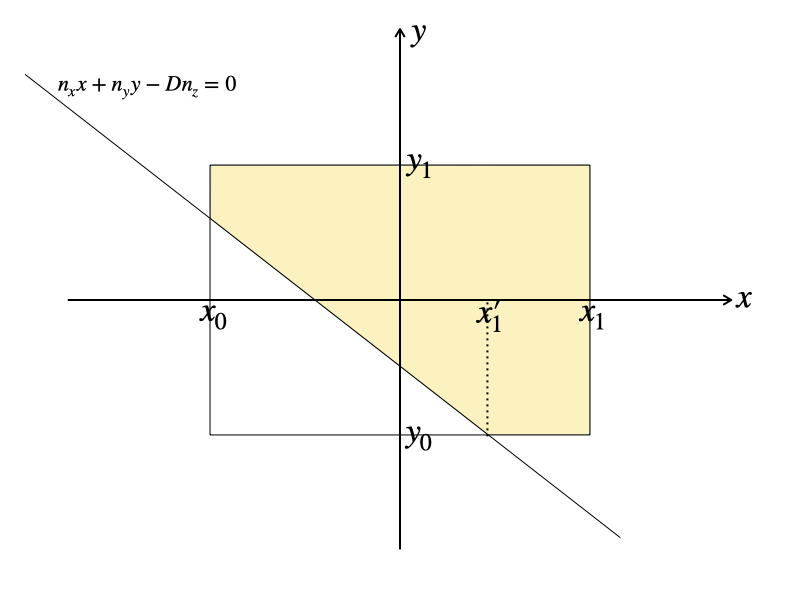
\begin{eqnarray*}
\frac{2I}{L_0} & = & D\int_{x_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – D\int_{x_0}^{x’_1}\!\!\! F(x, y(x))\,dx\ – D\int_{x’_1}^{x_1}\!\!\! F(x, y_0)\,dx \\
& = & \frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{y_1}{\sqrt{D^2+x_0^2}}+\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{x_0}{\sqrt{D^2+y_1^2}} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{y_1}{\sqrt{D^2+x_1^2}}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{x_1}{\sqrt{D^2+y_1^2}} \\
& & {}-\frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{y(x_0)}{\sqrt{D^2+x_0^2}}-\arctan\frac{n_yx_0-n_xy(x_0)}{D} \\
& & {}+\frac{Dn_x+n_zx(y_0)}{\sqrt{D^2+x(y_0)^2}}\arctan\frac{y_0}{\sqrt{D^2+x(y_0)^2}}+\arctan\frac{n_yx(y_0)-n_xy_0}{D} \\
& & {}-\frac{Dn_x+n_zx(y_0)}{\sqrt{D^2+x(y_0)^2}}\arctan\frac{y_0}{\sqrt{D^2+x(y_0)^2}}-\frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{x(y_0)}{\sqrt{D^2+y_0^2}} \\
& & {}+\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{y_0}{\sqrt{D^2+x_1^2}}+\frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{x_1}{\sqrt{D^2+y_0^2}} \\
& = & \frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{\sqrt{D^2+x_0^2}(y_1-y(x_0))}{D^2+x_0^2+y(x_0)y_1} \\
& & {}+\frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{\sqrt{D^2+y_0^2}(x_1-x(y_0))}{D^2+y_0^2+x(y_0)x_1} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{\sqrt{D^2+x_1^2}(y_1-y_0)}{D^2+x_1^2+y_0y_1} \\
& & {}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{\sqrt{D^2+y_1^2}(x_1-x_0)}{D^2+y_1^2+x_0x_1} \\
& & {}-\arctan\frac{D\{n_y(x(y_0)-x_0)+n_x(y(x_0)-y_0)\}}{(Dn_x+n_zx_0)(Dn_y+n_zy_0)-x_0y_0} \\
& = & \frac{Dn_x+n_zx_0}{\sqrt{D^2+x_0^2}}\arctan\frac{\sqrt{D^2+x_0^2}(n_xx_0+n_yy_1-Dn_z)}{n_y(D^2+x_0^2)+(Dn_z-n_xx_0)y_1} \\
& & {}+\frac{Dn_y+n_zy_0}{\sqrt{D^2+y_0^2}}\arctan\frac{\sqrt{D^2+y_0^2}(n_xx_1+n_yy_0-Dn_z)}{n_x(D^2+y_0^2)+(Dn_z-n_yy_0)x_1} \\
& & {}-\frac{Dn_x+n_zx_1}{\sqrt{D^2+x_1^2}}\arctan\frac{\sqrt{D^2+x_1^2}(y_1-y_0)}{D^2+x_1^2+y_0y_1} \\
& & {}-\frac{Dn_y+n_zy_1}{\sqrt{D^2+y_1^2}}\arctan\frac{\sqrt{D^2+y_1^2}(x_1-x_0)}{D^2+y_1^2+x_0x_1} \\
& & {}-\arctan\frac{D(n_xx_0+n_yy_0-Dn_z)}{(Dn_x+n_zx_0)(Dn_y+n_zy_0)-x_0y_0}
\end{eqnarray*}

