すべての積分を計算できたので、つなげてみましょう。
\begin{eqnarray*}
x’_0 & = & max\left(x_0,\ min\left(x_1,\ \frac{Dn_z\ – n_y y_1}{n_x}\right)\right),\\
x’_1 & = & min\left(x_1,\ max\left(x_0,\ \frac{Dn_z\ – n_y y_0}{n_x}\right)\right),\\
y(x) & = & \frac{Dn_z\ – n_x x}{n_y}
\end{eqnarray*}
として、
$$
I = L_0 \int_{x’_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – L_0 \int_{x’_0}^{x’_1}\!\!\! F(x, y(x))\,dx\ – L_0 \int_{x’_1}^{x_1}\!\!\! F(x, y_0)\,dx
$$
と書けたわけですが、少し場合わけをします。
まずは一番簡単な \(x’_0 = x’_1 = x_1\) の場合。
$$ I = 0 $$
次に簡単なのが、\(x’_0 = x’_1 = x_0\) の場合。積分区間が対象なので、積分結果も \(x\) と \(y\) の入れ替えに対して対象になっています。
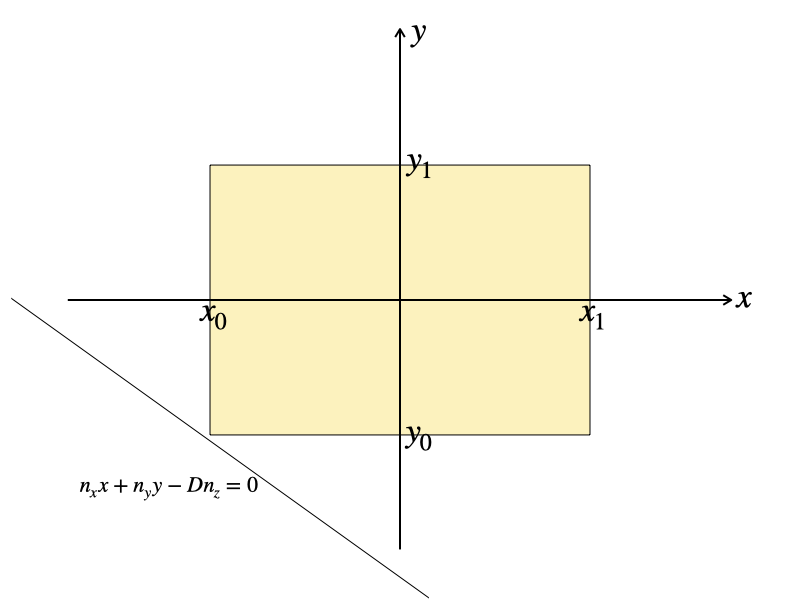
\begin{eqnarray*}
\frac{I}{L_0} & = & \int_{x_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – \int_{x_0}^{x_1}\!\!\! F(x, y_0)\,dx \\
& = & n_x \ln \frac{\left(\sqrt{D^2 + x_0^2 + y_1 ^2}\ + y_1\right)\left(\sqrt{D^2 + x_1^2 + y_0 ^2}\ + y_0\right)}{\left(\sqrt{D^2 + x_1^2 + y_1 ^2}\ + y_1\right)\left(\sqrt{D^2 + x_0^2 + y_0 ^2}\ + y_0\right)} \\
& + & n_y \ln\frac{\left(\sqrt{D^2 + x_0^2 + y_1^2} + x_0\right)\left(\sqrt{D^2 + x_1^2 + y_0^2} + x_1\right)}{\left(\sqrt{D^2 + x_1^2 + y_1^2} + x_1\right)\left(\sqrt{D^2 + x_0^2 + y_0^2} + x_0\right)} \\
& – & n_z \arctan \frac{x_1y_1}{D\sqrt{D^2 + x_1^2 + y_1^2}}\ + n_z \arctan \frac{x_0y_1}{D\sqrt{D^2 + x_0^2 + y_1^2}} \\
& + & n_z \arctan \frac{x_1y_0}{D\sqrt{D^2 + x_1^2 + y_0^2}}\ – n_z \arctan \frac{x_0y_0}{D\sqrt{D^2 + x_0^2 + y_0^2}}
\end{eqnarray*}
次は \(x’_0 = x_0,\ x’_1 = x_1\) の場合です。
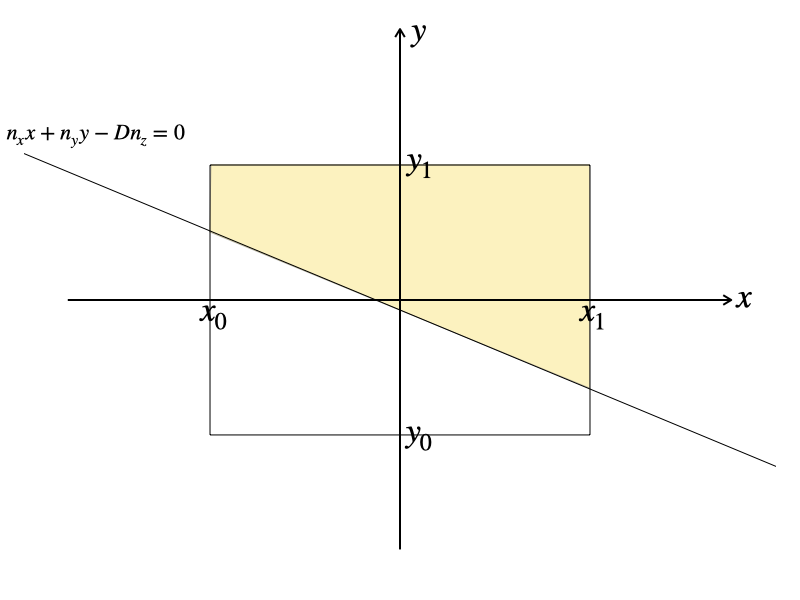
\begin{eqnarray*}
\frac{I}{L_0} & = & \int_{x_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – \int_{x_0}^{x_1}\!\!\! F(x, y(x))\,dx \\
& = & n_x \ln \frac{\left(\sqrt{D^2 + x_0^2 + y_1 ^2}\ + y_1\right) \left(\sqrt{D^2 + x_1^2 + y(x_1)^2} + y(x_1)\right)}{\left(\sqrt{D^2 + x_1^2 + y_1 ^2}\ + y_1\right)\left(\sqrt{D^2 + x_0^2 + y(x_0)^2} + y(x_0)\right)} \\
& + & n_y \ln\frac{\sqrt{D^2 + x_0^2 + y_1^2} + x_0}{\sqrt{D^2 + x_1^2 + y_1^2} + x_1} \\
& + & \sqrt{n_x^2 + n_y^2} \ln \frac{\left(\sqrt{(n_x^2 + n_y^2)(D^2 + x_1^2 + y(x_1)^2)} + n_y x_1\ – n_x y(x_1)\right)}{\left(\sqrt{(n_x^2 + n_y^2)(D^2 + x_0^2 + y(x_0)^2)} + n_y x_0\ – n_x y(x_0)\right)} \\
& – & n_z \arctan \frac{x_1y_1}{D\sqrt{D^2 + x_1^2 + y_1^2}}\ + n_z \arctan \frac{x_0y_1}{D\sqrt{D^2 + x_0^2 + y_1^2}} \\
& + & n_z \arctan\frac{Dn_x + n_z x_1}{n_y\sqrt{D^2 + x_1^2 + y(x_1)^2}}\ – n_z \arctan\frac{Dn_x + n_z x_0}{n_y\sqrt{D^2 + x_0^2 + y(x_0)^2}}
\end{eqnarray*}
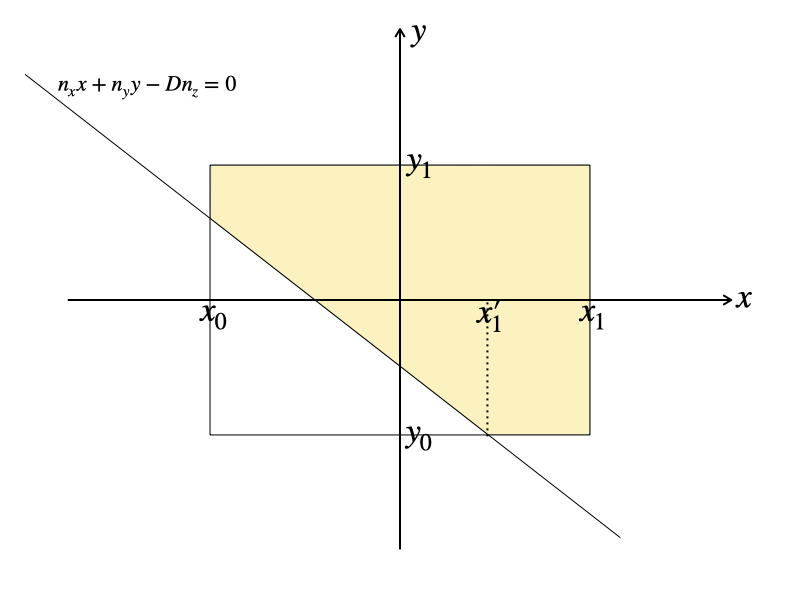
次は \(x_0 \le x’_0 \le x’_1 \le x_1\) の場合。
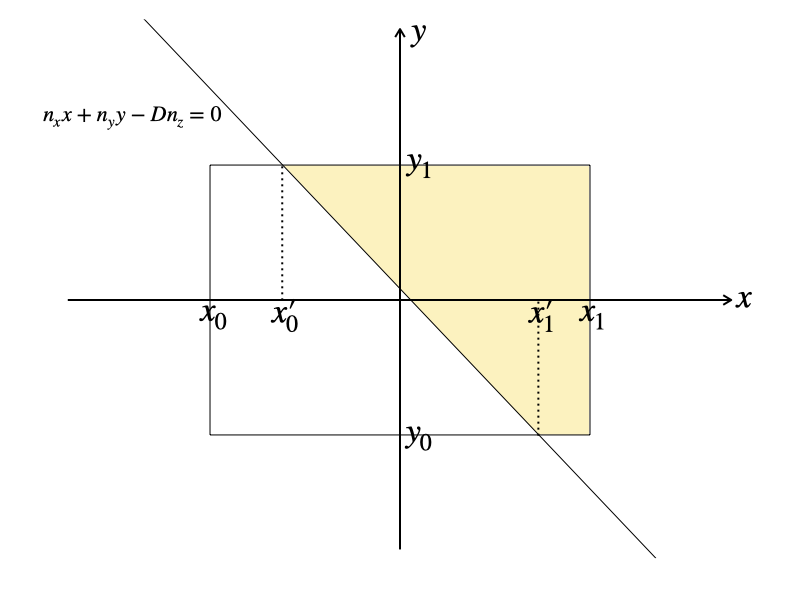
ここで、\(x’_0 = x(y_1),\ x’_1 = x(y_0),\ x(y) = \frac{Dn_z – n_y y}{n_x}\) と書くことにします。
\begin{eqnarray*}
\frac{I}{L_0} & = & \int_{x’_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – \int_{x’_0}^{x’_1}\!\!\! F(x, y(x))\,dx\ – \int_{x’_1}^{x_1}\!\!\! F(x, y_0)\,dx \\
& = & n_x \ln \frac{\sqrt{D^2 + x_1^2 + y_0 ^2}\ + y_0}{\sqrt{D^2 + x_1^2 + y_1 ^2}\ + y_1}\\
& + & n_y \ln\frac{\left(\sqrt{D^2 + x(y_1)^2 + y_1^2} + x(y_1)\right)\left(\sqrt{D^2 + x_1^2 + y_0^2} + x_1\right)}{\left(\sqrt{D^2 + x_1^2 + y_1^2} + x_1\right)\left(\sqrt{D^2 + x(y_0)^2 + y_0^2} + x(y_0)\right)} \\
& + & \sqrt{n_x^2 + n_y^2} \ln \frac{\left(\sqrt{(n_x^2 + n_y^2)(D^2 + x(y_0)^2 + y_0^2)} + n_y x(y_0)\ – n_x y_0\right)}{\left(\sqrt{(n_x^2 + n_y^2)(D^2 + x(y_1)^2 + y_1^2)} + n_y x(y_1)\ – n_x y_1\right)} \\
& – & n_z \arctan \frac{x_1y_1}{D\sqrt{D^2 + x_1^2 + y_1^2}}\ + n_z \arctan \frac{x_1y_0}{D\sqrt{D^2 + x_1^2 + y_0^2}} \\
& + & n_z \arctan \frac{x(y_1)y_1}{D\sqrt{D^2 + x(y_1)^2 + y_1^2}}\ – n_z \arctan\frac{Dn_x + n_z x(y_1)}{n_y\sqrt{D^2 + x(y_1)^2 + y_1^2}} \\
& – & n_z \arctan \frac{x(y_0)y_0}{D\sqrt{D^2 + x(y_0)^2 + y_0^2}} + n_z \arctan\frac{Dn_x + n_z x(y_0)}{n_y\sqrt{D^2 + x(y_0)^2 + y_0^2}}
\end{eqnarray*}
この場合、\(x\) 軸と \(y\) 軸を入れ替えると、積分範囲が \(x’_0 = x_0,\ x’_1 = x_1\) となるので、\(x\) と \(y\) を入れ替えたら \(x’_0 = x_0,\ x’_1 = x_1\) の場合と同じになるはずで、実際に \(\ln\) の項はそうなっているんですが、\(\arctan\) の項がおかしい。
$$ \arctan \frac{x(y)y}{D\sqrt{D^2 + x(y)^2 + y^2}} – \arctan \frac{Dn_x + n_zx(y)}{n_y\sqrt{D^2 + x(y)^2 + y^2}} = \arctan \frac{Dn_y + n_zy}{n_x\sqrt{D^2 + x(y)^2 + y^2}} $$
が成り立ってくれればいいんですが、三角関数の加法定理を使っていろいろ計算してみてもうまくいきませんでした。なので、もしかしたらどこかで計算間違いがあるのかもしれません。。。(何度も見直して積分自体は合ってると思うんですが)
次は \(x_0 \le x’_0 \le x’_1 = x_1\) の場合です。
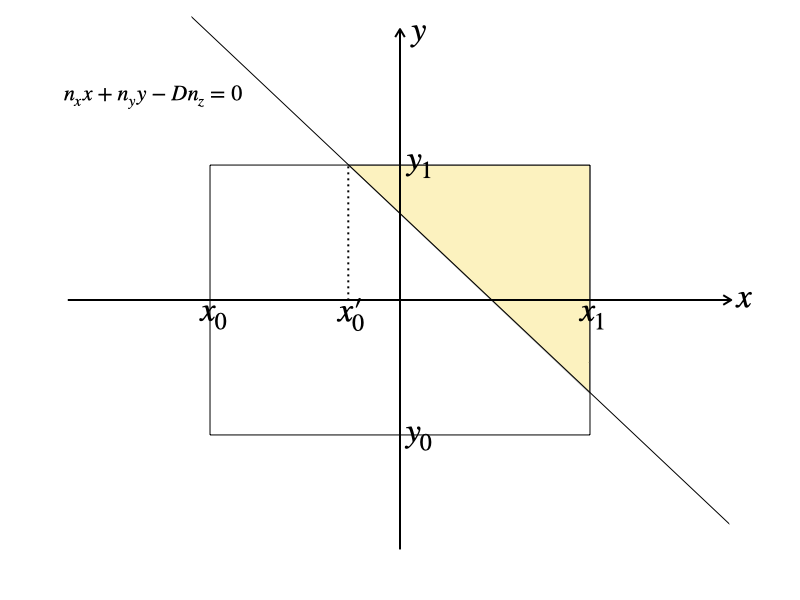
\begin{eqnarray*}
\frac{I}{L_0} & = & \int_{x’_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – \int_{x’_0}^{x_1}\!\!\! F(x, y(x))\,dx \\
& = & n_x \ln \frac{\sqrt{D^2 + x_1^2 + y(x_1)^2} + y(x_1)}{\sqrt{D^2 + x_1^2 + y_1 ^2}\ + y_1} \\
& + & n_y \ln\frac{\sqrt{D^2 + x(y_1)^2 + y_1^2} + x(y_1)}{\sqrt{D^2 + x_1^2 + y_1^2} + x_1} \\
& + & \sqrt{n_x^2 + n_y^2} \ln \frac{\left(\sqrt{(n_x^2 + n_y^2)(D^2 + x_1^2 + y(x_1)^2)} + n_y x_1\ – n_x y(x_1)\right)}{\left(\sqrt{(n_x^2 + n_y^2)(D^2 + x(y_1)^2) + y_1^2} + n_y x(y_1)\ – n_x y_1\right)} \\
& – & n_z \arctan \frac{x_1y_1}{D\sqrt{D^2 + x_1^2 + y_1^2}}\ + n_z \arctan \frac{x(y_1)y_1}{D\sqrt{D^2 + x(y_1)^2 + y_1^2}} \\
& + & n_z \arctan\frac{Dn_x + n_z x_1}{n_y\sqrt{D^2 + x_1^2 + y(x_1)^2}}\ – n_z \arctan\frac{Dn_x + n_z x(y_1)}{n_y\sqrt{D^2 + x(y_1)^2 + y_1^2}}
\end{eqnarray*}
積分区間が \(x\) 軸と \(y\) 軸の入れ替えに対して対象なので、積分結果も対象のはずですが、ここでも \(\arctan\) の項がおかしい。やはり
$$ \arctan \frac{x(y)y}{D\sqrt{D^2 + x(y)^2 + y^2}} – \arctan \frac{Dn_x + n_zx(y)}{n_y\sqrt{D^2 + x(y)^2 + y^2}} = \arctan \frac{Dn_y + n_zy}{n_x\sqrt{D^2 + x(y)^2 + y^2}} $$
が成り立つ必要があります。
最後に \(x_0 = x’_0 \le x’_1 \le x_1\) の場合。
\begin{eqnarray*}
\frac{I}{L_0} & = & \int_{x_0}^{x_1}\!\!\! F(x, y_1)\,dx\ – \int_{x_0}^{x’_1}\!\!\! F(x, y(x))\,dx\ – \int_{x’_1}^{x_1}\!\!\! F(x, y_0)\,dx \\
& = & n_x \ln \frac{\left(\sqrt{D^2 + x_0^2 + y_1^2}\ + y_1\right)\left(\sqrt{D^2 + x_1^2 + y_0^2}\ + y_0\right)}{\left(\sqrt{D^2 + x_1^2 + y_1^2}\ + y_1\right)\left(\sqrt{D^2 + x_0^2 + y(x_0)^2}\ + y(x_0)\right)} \\
& + & n_y \ln\frac{\left(\sqrt{D^2 + x_0^2 + y_1^2} + x_0\right)\left(\sqrt{D^2 + x_1^2 + y_0^2} + x_1\right)}{\left(\sqrt{D^2 + x_1^2 + y_1^2} + x_1\right)\left(\sqrt{D^2 + x(y_0)^2 + y_0^2} + x(y_0)\right)} \\
& + & \sqrt{n_x^2 + n_y^2} \ln \frac{\left(\sqrt{(n_x^2 + n_y^2)(D^2 + x(y_0)^2 + y_0^2)} + n_y x(y_0)\ – n_x y_0\right)}{\left(\sqrt{(n_x^2 + n_y^2)(D^2 + x_0^2 + y(x_0)^2)} + n_y x_0\ – n_x y(x_0)\right)} \\
& – & n_z \arctan \frac{x_1y_1}{D\sqrt{D^2 + x_1^2 + y_1^2}} + n_z \arctan \frac{x_1y_0}{D\sqrt{D^2 + x_1^2 + y_0^2}} \\
& – & n_z \arctan \frac{x(y_0)y_0}{D\sqrt{D^2 + x(y_0)^2 + y_0^2}} + n_z \arctan\frac{Dn_x + n_z x(y_0)}{n_y\sqrt{D^2 + x(y_0)^2 + y_0^2}} \\
& + & n_z \arctan \frac{x_0y_1}{D\sqrt{D^2 + x_0^2 + y_1^2}}\ -\ n_z \arctan\frac{Dn_x + n_z x_0}{n_y\sqrt{D^2 + x_0^2 + y(x_0)^2}}
\end{eqnarray*}
この場合も \(x\) 軸と \(y\) 軸の入れ替えに対して対象になるはずなんですが、やはり \(\arctan\) のところが少しおかしいようです。

