前回、エリアライトの積分を計算して Unity でベイクしたエリアライトと比較してみたところ、全然違う結果が得られて、そもそもエリアライトが点光源の集まりだと仮定したところが間違っていたのだろうと思い、再度積分計算にチャレンジしてみます。
座標系は前回同様に下図のようにとります。
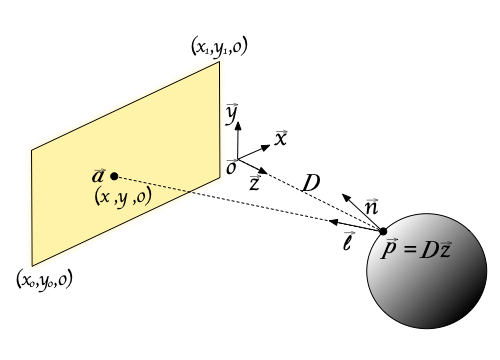
前回は、点 \(\vec{a}\) から出た光はどの方向にも一様な強さで放出されると仮定したんですが、どうもこれがいけなかったみたいなので、今回は、\(max(-\vec{l}\cdot\vec{z}, 0)\) の強さで放出されるとしてみます。ここで、\(\vec{l}\) は点 \(\vec{p}\) から点 \(\vec{a}\) の方向を向いた単位ベクトルで、
$$ \vec{l} = \frac{\vec{a}-\vec{p}}{|\vec{a}-\vec{p}|} = \frac{1}{\sqrt{D^2+x^2+y^2}}(x, y, -D) $$
と書けます。
すると、ディフューズの積分は
\begin{eqnarray*}
I & = & L_0 \int_{x_0}^{x_1}\!\!\!\!dx\int_{y_0}^{y_1}\!\!\!\!dy \frac{max(\vec{n}\cdot\vec{l}, 0) \,max(-\vec{z}\cdot\vec{l}, 0)}{|\vec{a}-\vec{p}|^2} \\
& = & L_0D\int_{x_0}^{x_1}\!\!\!\!dx\int_{y_0}^{y_1}\!\!\!\!dy \frac {max(xn_x+yn_y-Dn_z, 0)}{(D^2+x^2+y^2)^2}
\end{eqnarray*}
となります。ここで、\(D\) は積分変数に依存しない定数なので正の値としています(0 以下なら積分する必要なし)。
前回同様、\(max\) を \(y\) の積分区間に押しつけることにして、
$$ I = L_0D\int_{x_0}^{x_1}\!\!\!\!dx\int_{y’_0}^{y’_1}\!\!\!\!dy \frac {xn_x+yn_y-Dn_z}{(D^2+x^2+y^2)^2} $$
と書いて、先に \(y\) について積分します。
ここで、2種類の積分、
\begin{eqnarray*}
A & = & \int_{y’_0}^{y’_1}\!\!\frac{1}{(a^2 + y^2)^2}dy \\
B & = & \int_{y’_0}^{y’_1}\!\!\frac{y}{(a^2 + y^2)^2}dy
\end{eqnarray*}
を計算するがあるわけですが、前回同様、\(A\) は \(y = a\tan\theta\) とおけば簡単に積分できて、
\begin{eqnarray*}
A & = & \int_{y’_0}^{y’_1}\!\!\frac{1}{(a^2 + y^2)^2}dy \\
& = & \frac{1}{a^3}\int_{\theta_0}^{\theta_1}\!\!\cos^2\!\theta\,d\theta \\
& = & \frac{1}{2a^3}\left[ \sin\theta\cos\theta + \theta \right]_{\theta_0}^{\theta_1} \\
& = & \frac{1}{2a^3}\left[ \frac{ay}{a^2 + y^2} + \arctan\frac{y}{a} \right]_{y’_0}^{y’_1}
\end{eqnarray*}
\(B\) はもっと簡単に積分できて
\begin{eqnarray*}
B & = & \int_{y’_0}^{y’_1}\!\!\frac{y}{(a^2 + y^2)^2}dy \\
& = & -\frac{1}{2}\left[ \frac{1}{a^2 + y^2} \right]_{y’_0}^{y’_1}
\end{eqnarray*}
が得られます。
これを元の積分に戻してやります。
\begin{eqnarray*}
I & = & L_0D\int_{x_0}^{x_1}\!\!\!\left\{ (xn_x-Dn_z)A+n_yB \right\}dx \\
& = & \frac{L_0D}{2}\int_{x_0}^{x_1}\!\!\! \left\{ F(x, y’_1)-F(x, y’_0)\right\}dx, \\
F(x, y) & = & \frac{(xn_x-Dn_z)y}{(D^2+x^2)(D^2+x^2+y^2)}-\frac{n_y}{D^2+x^2+y^2}+\frac{xn_x-Dn_z}{(D^2 + x^2)^{\frac{3}{2}}}\arctan\frac{y}{\sqrt{D^2 + x^2}}
\end{eqnarray*}
前回同様に、\(0 \le n_x,\ n_y\) となるように座標系を選ぶことにすれば、積分区間は次の図のようになります。
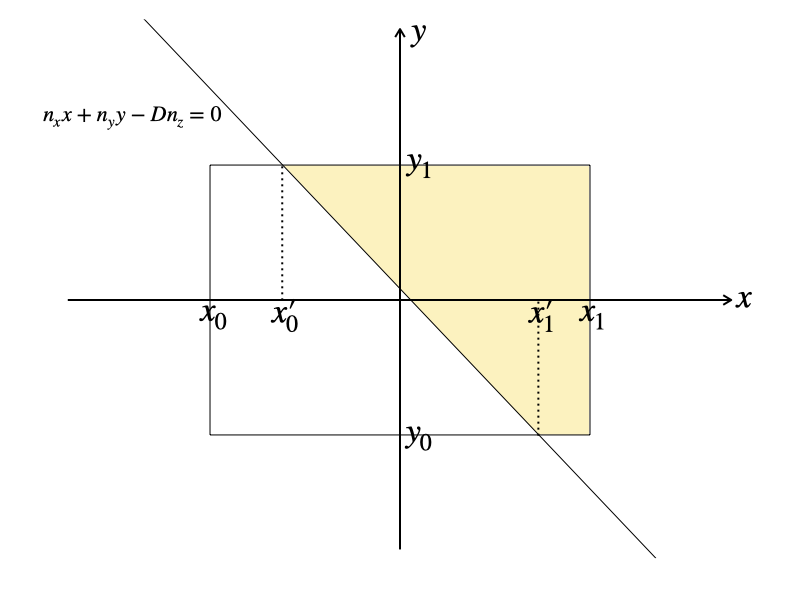
ここで、
\begin{eqnarray*}
x’_0 & = & max\left(x_0,\ min\left(x_1,\ \frac{Dn_z-n_y y_1}{n_x}\right)\right),\\
x’_1 & = & min\left(x_1,\ max\left(x_0,\ \frac{Dn_z-n_y y_0}{n_x}\right)\right)
\end{eqnarray*}
です。
そして、エリアライトの積分は次のように書けます。
$$ I = \frac{L_0D}{2}\int_{x’_0}^{x_1}\!\!\!F(x, y_1)\,dx-\frac{L_0D}{2}\int_{x’_0}^{x’_1}\!\!\!F(x, y(x))\,dx-\frac{L_0D}{2}\int_{x’_1}^{x_1}\!\!\!F(x, y_0)\,dx, \\
y(x) = \frac{Dn_z-n_x x}{n_y} $$
やはり \(y\) が定数(\(y_0\) もしくは \(y_1\)) の場合と、\(y = \frac{Dn_z-n_x x}{n_y}\) の場合で \(F(x, y)\) を積分する必要があるので、次のページでまず \(y\) が定数の場合を計算していきます。

