Unity のライトにはエリアライトというのがあって、下の図のように矩形(もしくは楕円)の上に一様に分布された光源を使うことができます。ただし、エリアライトは HDRP を除いてベイク専用で、ライトマップやライトプローブに焼き付けて使うことになります。このエリアライトにリアルタイムな影をつけてみようかなーと考えていて、そのためには、エリアライトの明るさを、おおざっぱでもいいので、リアルタイムで計算する必要がありました。
そこで、エリアライトの計算をやってみたのですが、ディフューズの計算自体はできたものの、Unity でライトマップにベイクした結果と比べると全然違う結果に…。とはいえ、それっぽい結果も得られたので、積分計算のやり方として、とりあえずブログに清書して残しておくことにしました。
正しいエリアライトの計算は次回のブログで!
ちなみに、 HDRP ではテクスチャ配列に入れたルックアップテーブルを使って実装しているみたいで、シェーダーで積分計算をしているわけではないみたいです。
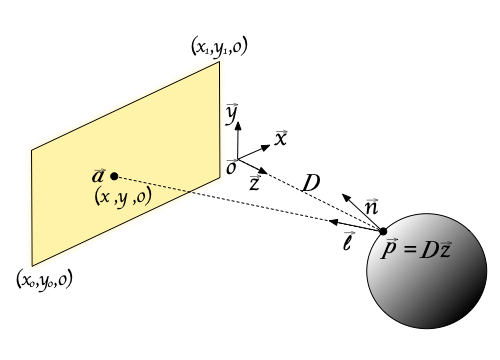
ある物体の表面上の点 \(\vec{p}\) でのディフューズ反射の値を計算することを考えます。その点での面の法線を \(\vec{n} = (n_x,\ n_y,\ n_z)\) として、被積分関数をなるべく簡単にするために、座標系を上の図のようにとります。\(x-y\) 平面上にエリアライトが分布していて、矩形の辺は \(x\) 軸と \(y\) 軸に平行です。また今回の計算ではベクトルの外積を使わないので、右手系か左手系かは気にせず、\(0 \le n_x,\ n_y\) となるように \(x\) 軸と \(y\) 軸の向きを決めることにします。
原点は点 \(\vec{p}\) を \(x-y\) 平面に垂直に投影した場所にあるとします。つまり、点 \(\vec{p}\) から \(x-y\) 平面までの距離を \(D\) とすると
$$ \vec{p} = D \vec{z} $$
となります。エリアライト上の点 \(\vec{a}\) を \(\vec{a} = (x, y, 0)\), 点 \(\vec{p}\) から点 \(\vec{a}\) の方向を向いた単位ベクトルを \(\vec{l}\) すると、\(\vec{l}\) は
$$ \vec{l} = \frac{\vec{a}-\vec{p}}{|\vec{a}-\vec{p}|} = \frac{1}{\sqrt{D^2+x^2+y^2}}(x, y, -D) $$
となり、点 \(\vec{p}\) でのディフューズの値 \(I\) は
$$ I = \int_{x_0}^{x_1}\!\!\!\!dx\int_{y_0}^{y_1}\!\!\!\!dy \frac{L_0 max(\vec{n}\cdot\vec{l}, 0)}{|\vec{a}-\vec{p}|^2} = L_0\int_{x_0}^{x_1}\!\!\!\!dx\int_{y_0}^{y_1}\!\!\!\!dy \frac {max(xn_x+yn_y-Dn_z, 0)}{(D^2+x^2+y^2)^{\frac{3}{2}}} $$
となります。ここで、\(L_0\) はライトの明るさ(色)を表わすパラメーターで、点 \(\vec{a}\) から出た光はどの方向にも一様な強さで、距離の2乗に反比例して減衰するとしています (どうも「どの方向にも一様な」という前提が違っていたみたいで、最後のページで Unity のベイクしたエリアライトと比較したところ、違う結果になってしまいました)。また、\(x_0 \lt x_1,\ y_0 \lt y_1\) とします。
\(max\) がやっかいですが、\(y\) の積分区間に押し付けて
$$ I = L_0\int_{x_0}^{x_1}\!\!\!\!dx\int_{y’_0}^{y’_1}\!\!\!\!dy \frac {xn_x+yn_y-Dn_z}{(D^2+x^2+y^2)^{\frac{3}{2}}} $$
と書くことにします。積分区間 \([y’_0, y’_1]\) は \(x\) の関数となる場合があるので、先に \(y\) について積分します。
2種類の積分
\begin{eqnarray*}
A & = & \int_{y’_0}^{y’_1}\!\!\frac{1}{(a^2 + y^2)^{\frac{3}{2}}}dy \\
B & = & \int_{y’_0}^{y’_1}\!\!\frac{y}{(a^2 + y^2)^{\frac{3}{2}}}dy
\end{eqnarray*}
を計算するがあるわけですが、順番にやっていきます。
まずは簡単な \(B\) の方。
\begin{eqnarray*}
B & = & – \left[ \frac{1}{\sqrt{a^2 + y^2}} \right]_{y’_0}^{y’_1} \\
& = & \frac{1}{\sqrt{a^2 + {y’_0}^2}}-\frac{1}{\sqrt{a^2+{y’_1}^2}}
\end{eqnarray*}
次に \(A\) の積分ですが、\(y = a\tan\theta\) とおくと
\begin{eqnarray*}
& dy & = & \frac{a}{\cos^2\theta} d\theta, \\
& a^2+y^2 & = & \frac{a^2}{\cos^2\theta}
\end{eqnarray*}
となるので、\(y’_0 = a\tan\theta_0,\ y’_1 = a\tan\theta_1 \) とすると、
\begin{eqnarray*}
A & = & \int_{\theta_0}^{\theta_1}\frac{\cos\theta}{a^2} d\theta \\
& = & \frac{1}{a^2}\left\{\sin\theta_1-\sin\theta_0 \right\} \\
& = & \frac{1}{a^2}\left\{\frac{y’_1}{\sqrt{a^2+{y’_1}^2}}-\frac{y’_0}{\sqrt{a^2+{y’_0}^2}} \right\}
\end{eqnarray*}
が得られます。\(a^2 = D^2+x^2\) として元の積分に \(A, B\) を戻してやると、
\begin{eqnarray*}
I & = & L_0\int_{x_0}^{x_1}\!\!\!\left\{ (xn_x-Dn_z)A+n_yB \right\}dx \\
& = & L_0\int_{x_0}^{x_1}\!\!\! \left\{ F(x, y’_1)-F(x, y’_0)\right\}dx, \\
F(x, y) & = & \frac{1}{\sqrt{D^2+y^2+x^2}}\left(\frac{n_xyx-Dn_zy}{D^2+x^2}-n_y\right)
\end{eqnarray*}
です。\(y\) についての積分はそれほど難しくありませんね。もしエリアライトが \(x\) 軸に沿って棒状に分布していれば、\(x\) について積分する必要がないので、シェーダーで計算するのも現実的です。
次に、\(x\) について積分する前に、積分範囲について整理しておきましょう。\(0 \le n_x,\ n_y\) となるように座標系を選んだので、積分範囲は次の図の台形のような形になります。
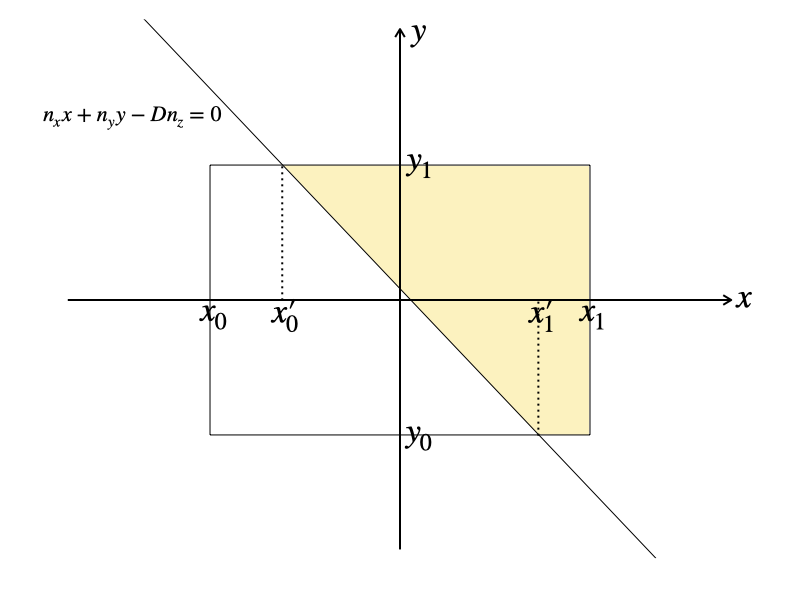
ここで、
\begin{eqnarray*}
x’_0 & = & max\left(x_0,\ min\left(x_1,\ \frac{Dn_z-n_y y_1}{n_x}\right)\right),\\
x’_1 & = & min\left(x_1,\ max\left(x_0,\ \frac{Dn_z-n_y y_0}{n_x}\right)\right),\\
y(x) & = & \frac{Dn_z-n_x x}{n_y}
\end{eqnarray*}
とすると、積分範囲は次のように書けます。
$$ I = L_0\int_{x’_0}^{x_1}\!\!\!F(x, y_1)\,dx-L_0\int_{x’_0}^{x’_1}\!\!\!F(x, y(x))\,dx-L_0\int_{x’_1}^{x_1}\!\!\!F(x, y_0)\,dx $$
つまり、\(y\) が定数(\(y_0\) もしくは \(y_1\)) の場合と、\(y = \frac{Dn_z-n_x x}{n_y}\) の場合で \(F(x, y)\) を積分する必要があります。
次のページでは、\(y\) が定数の場合を計算していきます。

